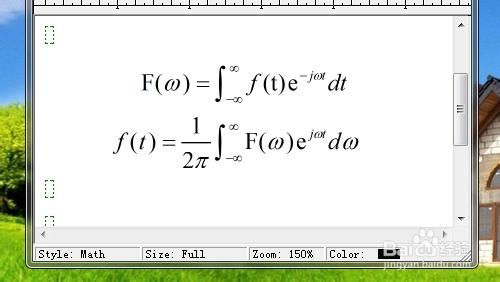傅立葉變換常常應用於在信號處理,其在信號處理中有著很重要的位置。下面我們就介紹一種最簡單的傅立葉變換,即單位階躍函數的傅立葉變換。然後用matlab實現單位階躍函數的傅立葉變換。
工具/原料
matlab 軟件
正常電腦
方法/步驟
傅立葉變換簡介
傅立葉變換是一種線性的積分變換,常在將信號在時域(或空域)和頻域之間變換時使用,在物理學和工程學中有許多應用。時域中的信號函數f(t)與他在頻域中的傅立葉變換F(w)可用如下圖的數學表達式表示他們之間的關係。
函數指令簡介
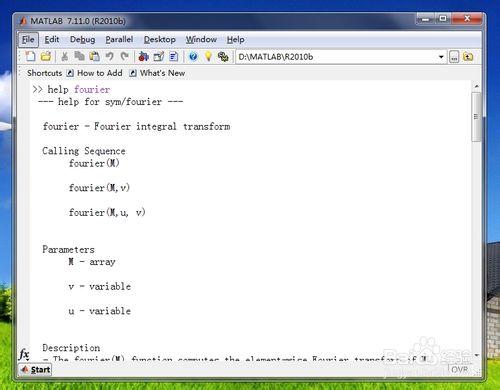
在matlab中提供了兩種完成傅立葉變換的途徑,可以直接調用指令fourier和ifourier進行傅立葉變換。此外用戶還可以利用第一步的定義,利用積分指令int進行傅立葉變換。下面是fourier和ifourier指令的調用語法。下圖是matlab提供的幫助信息。
Fw=fourier(ft,t,w) %求“時域”函數ft的Fourier變換Fw
ft=ifourier(Fw,w,t) %求“頻域”函數Fw的Fourier反變換ft
利用指令求傅立葉變換
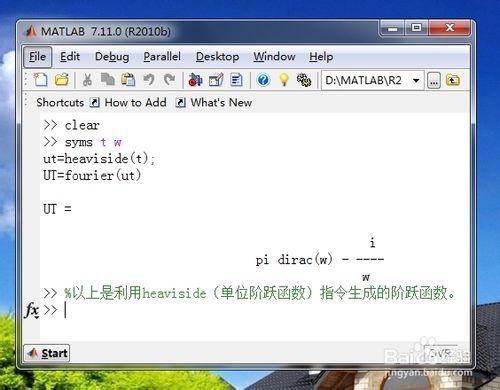
這裡我們先用heaviside(單位階躍函數)指令生成了單位階躍函數,然後用fourier指令進行傅立葉變換。具體指令及結果如下(下圖):
syms t w
ut=heaviside(t);
UT=fourier(ut)
求傅立葉反變換進行驗算
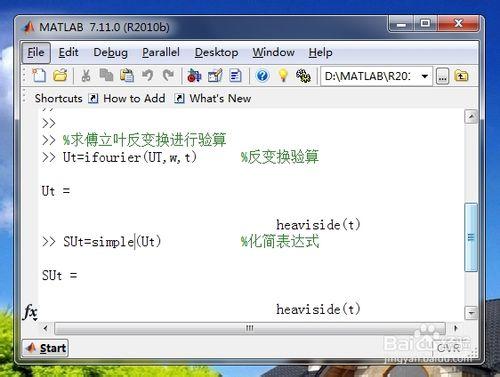
這一步我們用反傅立葉變換指令ifourier,進行反變換來驗證,然後簡化表達式。結果如下圖:
Ut=ifourier(UT,w,t)
SUt=simple(Ut)
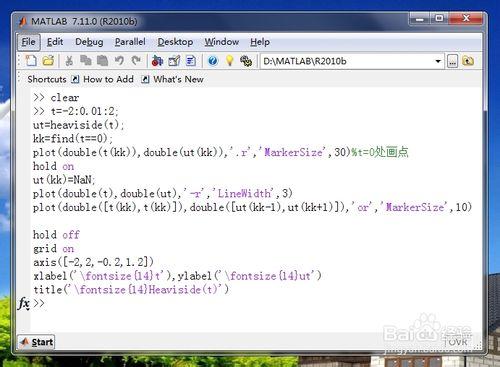
畫單位階躍函數曲線(代碼)代碼如下:
t=-2:0.01:2;
ut=heaviside(t);
kk=find(t==0);
plot(double(t(kk)),double(ut(kk)),'.r','MarkerSize',30)
hold on
ut(kk)=NaN;
plot(double(t),double(ut),'-r','LineWidth',3)
plot(double([t(kk),t(kk)]),double([ut(kk-1),ut(kk+1)]),'or','MarkerSize',10)
hold off
grid on
axis([-2,2,-0.2,1.2])
xlabel('\fontsize{14}t'),ylabel('\fontsize{14}ut')
title('\fontsize{14}Heaviside(t)')
畫單位階躍函數曲線(圖像)下圖就是 Heaviside(t) 定義的單位階躍函數。
注意事項
如果本經驗對你有幫助,記得點有用、收藏、評論哦!歡迎點擊右邊,分享給好友!