常見的基本幾何體的三視圖
一、畫基本體三視圖的方法步驟
1 .確定三個視圖的位置。選擇立體上的一個點或立體的對稱中心線、主要稜線、平面等作為畫圖參考基準;先畫出它們的三個視圖(布圖),注意要做到橫平豎直。
2 .畫出反映立體主要形狀特徵(實形)的視圖。
3 .再根據立體的長、寬、高尺寸(相對座標),依照“長對正、高平齊、寬相等”的規律,完成另外兩個視圖。
4 .視圖完成後,應擦去作圖輔助線。
· 立體是具有三維座標的實心體,研究的立體投影是研究立體表面的投影。
· 立體是有具體形狀和尺寸大小的形體。畫三視圖時,主要用長、寬、高方向的相對座標,與投影軸無關,從這裡開始不再畫出投影軸。
二、平面基本體
1.稜柱
⑴ 稜柱的組成
由上下兩個底面和若干側稜面組成。側稜面與側稜面的交線叫側稜線,側稜線相互平行。
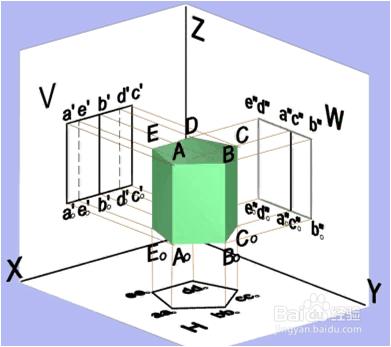
⑵ 五稜柱的三視圖
(1)布圖:選點AO畫圖參考基準,畫出其三個投影圖。
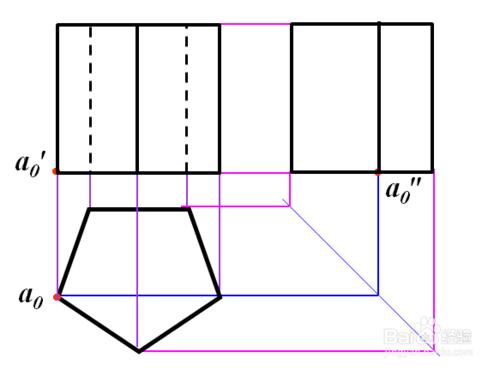
(2) 畫出反映立體主要形狀特徵的俯視圖。
(3) 由“長對正”和立體的高度畫出主視圖。
(4)利用“寬相等”和"高平齊”畫出左視圖(二求三)。
2.稜錐
⑴ 稜錐的組成
由一個底面和若干側稜面組成。側稜線交於有限遠的一點——錐頂。
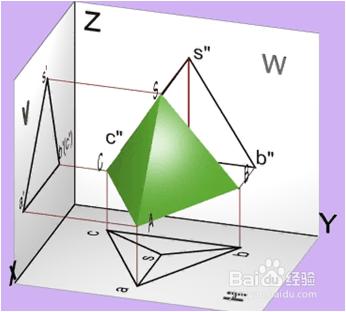
⑵ 三稜錐的三視圖
稜錐處於圖示位置時,其底面 ABC是水平面,在俯視圖上反映實形。側稜面SBC為正垂面,另兩個側稜面為一般位置平面。
(1)布圖: 選點A為畫圖參考基準,畫出其三個投影圖。
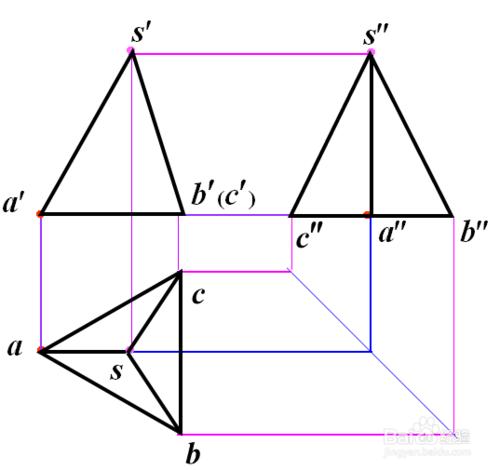
(2) 畫出反映底面實形的底面及錐頂 S的水平投影。
(3) 由“長對正”和立體的高度畫出主視圖。
4)利用“寬相等” 稜錐處於圖示位置時,其底面 ABC是水平面,在俯視圖上反映實形。側稜面SBC為正垂面,另兩個側稜面為一般位置平面。和"高平齊”畫出左視圖(二求三)。
三、迴轉體
1.圓柱體
⑴ 圓柱體的組成
圓柱體由圓柱面和兩個底面組成。
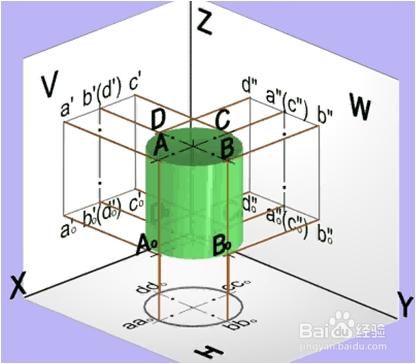
⑵ 圓柱體的三視圖
其中:圓柱面是由直線AA1繞與它平行的軸線OO1旋轉而成。直線 AA1稱為母線。圓柱面上與軸線平行的任一直線稱為圓柱面的素線.
⑶ 輪廓線素線的投影分析與曲面的可見性的判斷
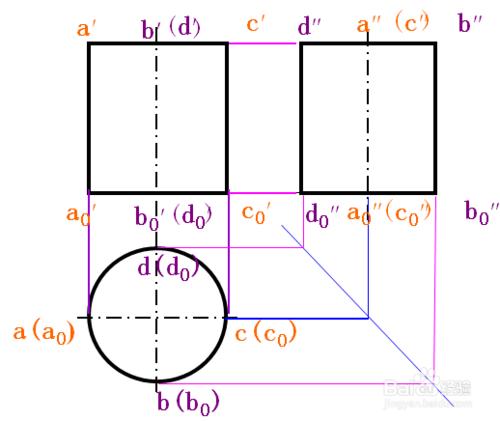
(1)布圖:選迴轉軸和底面稜線為畫圖參考基準。
(2) 畫出反映立體主要形狀特徵的俯視圖。
(3) 由“長對正”和立體的高度畫出主視圖。
(4)利用“寬相等”和"高平齊”畫出左視圖(二求三)。
2.圓錐體
⑴ 圓錐體的組成
圓錐體由圓錐面和底面組成。
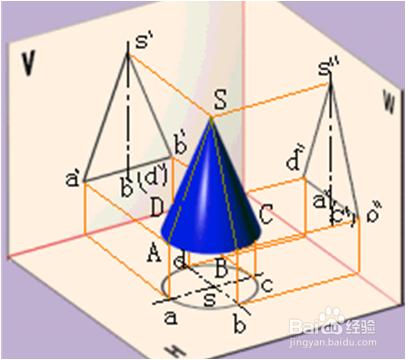
⑵ 圓錐體的三視圖
其中:圓錐面是由直線SA繞與它相交的軸線OO1旋轉而成。S 稱為錐頂,直線SA稱為母線。圓錐面上過錐頂的任一直線稱為圓錐面的素線。
⑶ 輪廓線素線的投影分析
與曲面的可見性的判斷
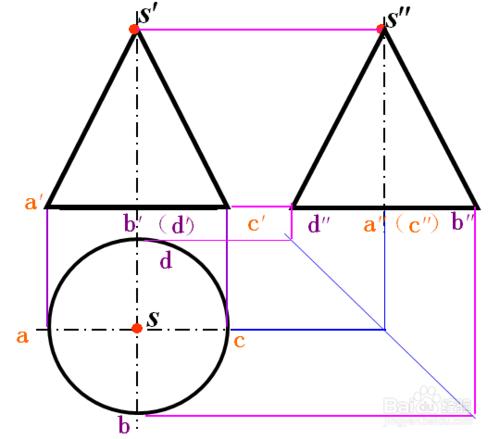
(1)布圖:選迴轉軸和底面稜線為畫圖參考基準。
(2) 畫出反映立體主要形狀特徵的俯視圖。
(3) 由“長對正”和立體的高度畫出主視圖。
(4)利用“寬相等”和"高平齊”畫出左視圖(二求三)。
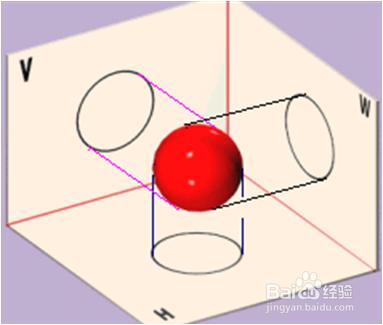
3.圓球
⑴ 圓球體的形成
球體的表面是球面。
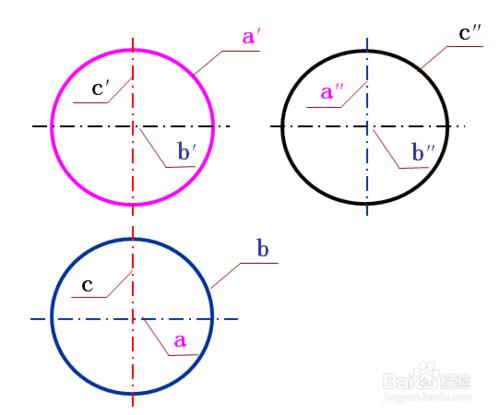
⑵ 圓球的三視圖
⑶ 輪廓線其中:球面是圓母線以它的直徑為軸旋轉而成。的投影與曲
面可見性的判斷
(1) 布圖:選三個圓的對稱中心線作為畫圖的參考基準;
(2) 畫出球體的主視圖——圓;
(3) 畫出球體的俯視圖——圓;
(4) 畫出球體的左視圖——圓;
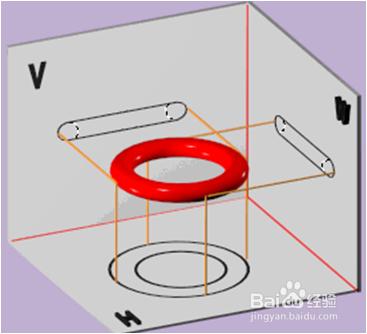
4.圓環
⑴ 圓環體的形成
圓環體的表面是環面。
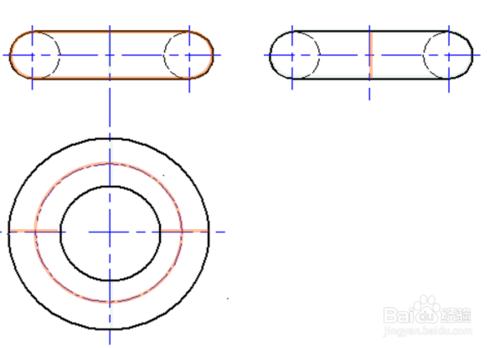
⑵ 圓環的三視圖
其中:環面是圓母線繞圓所在平面上,且在圓外的一直線為軸旋轉而成。
⑶ 輪廓線的投影與曲面可見性的判斷
輪廓線素線的投影分析與曲面的可見性的判斷
(1) 前半外環面的投影可見,後半外環面和內環面的投影不可見;
(2) 上半外、內環面的投影的投影可見,下半環面的投影不可見;
(3)左半外環面的投影可見,右半外環面和內環面的投影不可見;