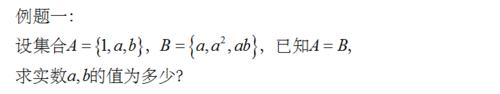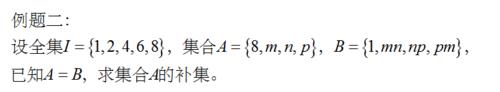如何利用數集的相等且有限性質解題?

兩個集合相等，是指的是第一個集合的元素 都出現在第二個集合裡，而第二個集合的元素也 都出現在第二個集合裡，則這兩個集合相等。兩個集合相等的另一種表述是，若兩個集合互為子集，則稱這兩個集合相等。

由集合相等的定義可以知道，兩個相等且有限的集合具有如下性質：兩個集合的元素之和相等，元素之積相等，元素個數相等。下面我們看看如何利用這幾條性質求解相關的集合例題。

工具/原料

高中集合知識

集合相等且有限的概念

例題一

例題一：

設集合A={1,a,b}，B={a,a^2,ab}，已知A=B，求實數a,b的值為多少？下圖為圖片格式的例題題目。

例題一解題過程：

由已知可知集合A，B有限且A=B，我們可以根據集合相等且有限的性質來進行問題的求解。下圖為例題一的解題過程。

例題二

例題二：

設全集I={1,2,4,6,8},集合A={8,m,n,p}，B={1,mn,np,pm}，已知A=B，求集合A的補集。下圖為圖片格式的例題二題目。

例題二解題過程：

由已知可知集合A，B有限且A=B，由全集已知，可知A=B的元素只能是全集中的某些元素，我們可以根據集合相等且有限的性質來進行問題的求解。下圖為例題二的解題過程。

例題三

例題三：

設集合A={1,a,a^2}，集合B={1,a,b}，已知A並B={a^2,b,b/2,b/6}，求集合A與B的並集。下圖為圖片格式的例題三題目。

例題三解題過程：

由已知可知集合A，B元素個數都為3個，有兩個元素相同，已知它們的並集是4個元素，故集合A和集合B的第三個元素不能相等。從而可得A與B 的並集，得到的並集與已知並集相等，我們可以根據集合相等且有限的性質來進行求解。下圖為例題三的解題過程。

注意事項

注意與元素互異性結合使用，可以使求解由元素之和相等，和元素之積相等得到的方程組變得簡單。