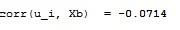經過一年的學習對Stata面板資料處理有了一定了解。在這裡將學習經驗分享給大家。
方法/步驟
短面板處理
面板資料是指既有截面資料又有時間序列的資料,因此其存在截面資料沒有的優勢,在用stata進行面板資料的估計時,一般選擇xtreg命令進行擬合。本節主要論述短面板的stata實現,即時間維度T相對於截面數n較小的資料。在那種情況下,由於T較小,每個個體的資訊較少,故無從討論擾動項是否存在自相關,我們一般假設其獨立同分布。
面板資料維度的確定
在面板資料進行模型估計前,要進行面板資料的維度確定。由於面板資料既有截面資料又有時間序列,而stata不能自動識別,因此,必須使得stata得知哪一部分是截面資料,而哪一部分是時間序列。
設定面板資料維度的基本命令為:
xtset panelvar timvar [, tsoptions]
其中panelvar代表截面資料變數,timvar代表時間序列變數。
選取某一面板資料進行維度設定(該資料研究職業培訓津貼對廠商廢棄率的影響):
xtset fcode year
固定效應估計
xtreg可以估計固定效應與隨機效應,兩者的差異在於選項的不同。
xtreg用來做固定效應的語法是:
xtreg depvar [indepvars] [if] [in] [weight] , fe [FE_options]
其語法可以help xtreg獲得。(說明,其中xt表示面板資料的命令,因此,在stata中輸入help xt可以學習面板資料描述、估計等命令。)
選取某一資料進行擬合:
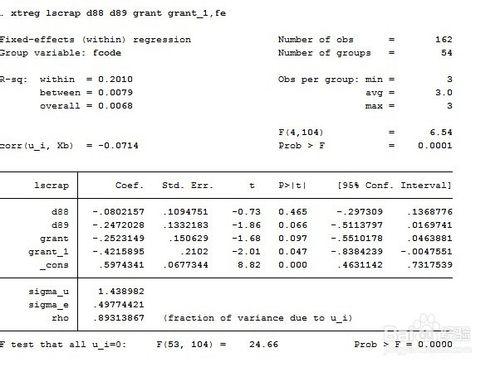
xtreg lscrap d88 d89 grant grant_1,fe
結果顯示如下:
其中,(1)表示組內、組間、總體的R方,其中固定效應看組內R-sq,隨機效應看總體R-sq。
(2)表示個體效應與解釋變數的相關係數。
(3)F檢驗表示模型整體顯著性。
(4)U表示個體觀測效應,sigma_u為個體效應的標準差
E表示隨機干擾項,u+e為所謂的混合誤差,rho是指個體效應的方差佔混合誤差方差的比重。
備註:(1)(2)(3)(4)分別對應一下的四張照片
隨機效應估計
xtreg用來做隨機效應的語法是:
xtreg depvar [indepvars] [if][in] [weight] , re [RE_options]
與上一部分類似的估計
xtreg lscrap d88 d89 grantgrant_1,re
(1)
與固定效應不同的是,固定效應F檢驗處,此處為瓦爾德卡方檢驗,同樣表示模型整體顯著性。
固定效應與隨機效應的選擇:豪斯曼檢驗
首先,看兩個效應的區別
固定效應與隨機效應的區別
區別一:
FE / RE 模型可統一表述為: y_it = u_i + x_it*b + e_it
對於FE,個體效應 u_i 被視為一組解釋變數,為非隨機變數,即 N-1 個虛擬變數;對於RE,個體效應 u_i被視為干擾項的一部分,因此是隨機變數,假設其服從正態分佈,即 u_i~N(0, sigma_u^2); 在上述兩個模型的設定中,e_it都被視為“乾乾淨淨的”干擾項,也就是OLS時那個揹負著眾多假設條件,但長相極為俊俏的干擾項,e_it~N(0,sigma_e^2)。 需要注意的是,在 FE 模型中,只有一個干擾項 e_it,它可以隨公司和時間而改變,所有個體差異都採用 u_i 來捕捉。而在 RE 模型中,其實有兩個干擾項:u_i 和 e_it,差別在於,第一種干擾項不隨時間改變(這也是所謂的“個體效應”的含義),而第二類干擾項可以隨時間改變。 因為上述對 FE 和 RE 中個體效應 u_i 的假設之差異,二者的估計方法亦有差異。FE可直接採用OLS估計,而RE則必須使用GLS才能獲得更為有效的估計量。
固定效應模型中的個體差異反映在每個個體都有一個特定的截距項上;隨機效應模型則假設所有的個體具有相同的截距項,個體的差異主要反應在隨機干擾項的設定上 。
區別二:
固定效應更適合研究樣本之間的區別,而隨機效應適合由樣本來推斷總體特徵。
其次,Hausman檢驗確定模型形式的選擇。
以上面的面板資料為例
xtreg lscrap d88 d89 grant grant_1,fe
est store fe
xtreg lscrap d88 d89 grant grant_1,re
est store re
hausman fe
結果顯示:
(1)
原假設為隨機效應,而最終P值為0.7096,接受原假設,模型最終選擇為隨機效應。