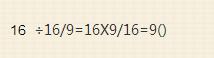分數應用題是小學數學中比較難的題,對於一些單位"1"變化的應用題就更難了.這時我們可以把單位"1",轉化為不變量為單位"1",根據題意找到數量對應的佔單位"1"的幾分之幾,求出問題.
方法/步驟
理解題意:已知條件是:一堆糖果,其中奶糖佔9/20,再放入16塊水果糖後,奶糖就只佔1/4,問題是:這一堆糖果原來有多少塊?
分析題意:在這道題中,兩個分數的單位"1"都是總糖塊,但是水果糖放入了16塊,那麼糖塊總數和水果糖的塊數都在變,只有奶糖沒變,那麼我們就要轉化為奶糖塊數為單位"1",原來奶糖佔9/20,奶糖是9份,水果糖就是20-9=11份,水果糖是奶糖的
11/9,放入16塊水果糖後,奶糖佔1/4,奶糖1份,水果糖4-1=3份,水果糖是奶糖的3倍.
16塊水果糖佔奶糖的幾分之幾,用現在3倍減去原來的11/9.
用16除以佔奶糖對應的分率,可以求出奶糖的塊數。
原來水果糖的塊數是奶糖的11/9,用奶糖的塊數乘這個分數就是水果糖原來的塊數。
原來這堆糖塊一共有多少,水果糖和奶糖一共的塊數。
全過程。
檢驗。把結果當已知條件,代入原題演算,和每個已知條件符合就正確。
小結。像這種情況的單位“1”轉化,就得以不變量為單位“1”,把其他量轉化為單位“1”的幾分之幾,再求出答案。在做完後要檢驗。
注意事項
找準不變量,哪個量不增加也不減少就是不變量。
數量除以對應的分率才正確。