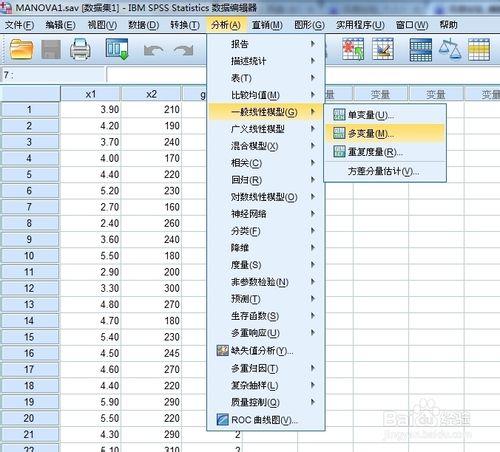
同單變量方差分析的思路是相同的,單變量方差分析是用於多組單變量均數的較多,主要思想是對方差進行分解。多元方差分析用於多組均向量的比較,主要思想是對方差-協方差矩陣的分解。
適用於各種形式的實驗設計的多組均向量比較、多變量因素分析和多變量回歸分析。
步驟:
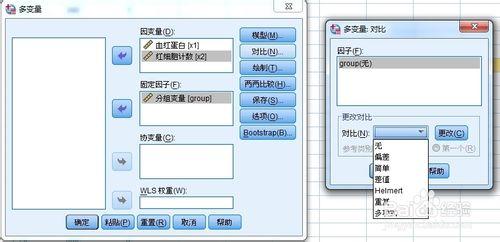
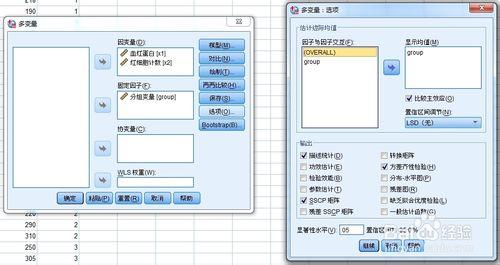
調出相關操作窗口,見圖片。
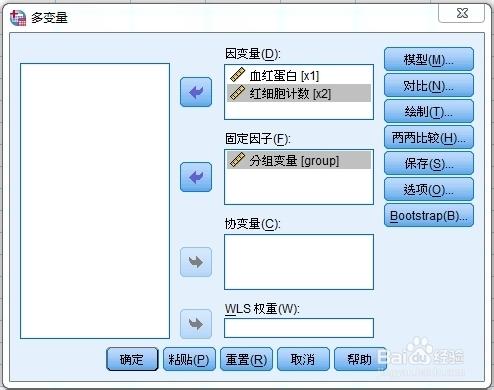
因變量:至少2個以上,且是數值變量。
固定因素:適用於固定效應模型,為分類變量,選一個或幾個。
協變量:與因變量有關的數值變量,協方差分析時才用。
WLS權重:變量加權,用於加權最小二乘分析。
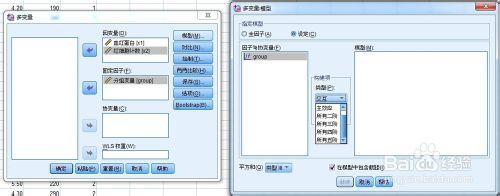
指定模型:系統默認是“全因子”,包含所有因子的主效應、所有協變量的主效應、所有因子的交互效應,但不含協變量交互效應。“設定”則為用戶自己定義,因素交互作用、因素和協變量間的交互效應,所有因素和協變量均含在模型中。
“因子與協變量”中,F表示固定因素,C表示協變量。
“交互”:所有因素不同水平各種組合的交互效應,系統默認。
“主效應”:只考慮主效應,不考慮交互效應。
“所有三階”:考慮3個因素的交互效應,其他幾階解釋同於此理。
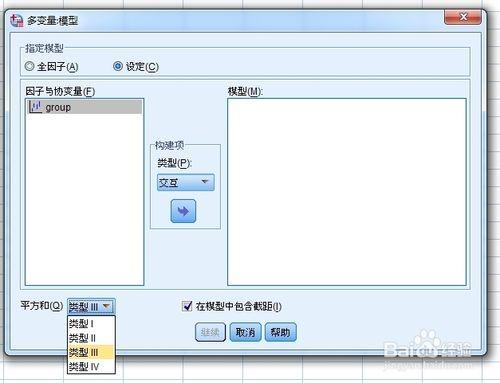
計算離差平方和:共有4種,系統默認“類型3”,“類型3”是最多應用的方法。
“類型1”:平衡設計,確定一級交互效應之前必須先確定主效應的離差,確定二級交互效應之前必須先確定一級交互效應離差,其他同理;多項式迴歸模型,其中,高次項確定前先確定低次項;嵌套模型,一級效應嵌套於二級效應之中,二級嵌套於三級之中,依次類推。
“類型2”:平衡的方差分析模型、僅含主效應模型、所有迴歸模型、純嵌套模型。
“類型3”:類型1和類型2所列的模型、沒有缺失數據的平衡或非平衡設計資料。
“類型4”:有缺失數據的平衡或非平衡設計資料、類型1和類型2所列的模型。
系統默認模型內含有截距。
“對比”:單變量組間比較,共6中方法供選擇。
“偏差”:將每個水平的均數與所有水平的總均數進行比較。
“簡單”:將各水平的均數與指定水平的均數進行比較。特別適合有對照的設計。
“差值”:將每個水平的均數與前一水平的均數進行比較(第一水平除外)。
“Helmert”:將每個水平的均數與後一水平的均數進行比較(最後一個水平除外)。
“重複”:將每個水平的均數與其後各水平的均數進行比較(最後一個水平除外)。
“多項式”:比較線性效應,二次效應、三次效應等,用於估計多項式趨勢。
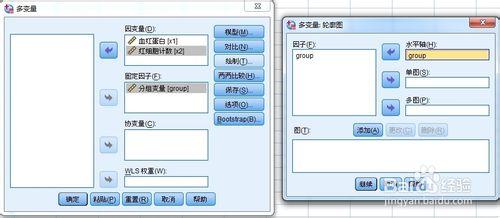
某因素某個水平上某因變量的估計均數,散點聯線後顯示估計均數隨兩個因素不同水平組合的變化趨勢,若平行線條,表示兩因素沒有交互作用,若有交叉,存在交互作用。用於比較模型中的因變量均數估計。
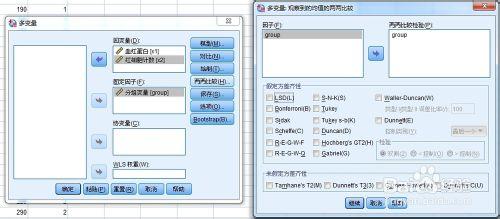
“兩兩比較”:具體操作可見我以前寫的文章,搜索“spss教程:單因素方差分析 ”。
因子與因子交互:選入預估計條件總體均數的主效應和交互效應的因素,並選入右框“顯示均值”,顯示框內因素的條件均數估計、包括均數、標準誤、可信區間。
“比較主效應”:提供模型中各主效應的條件估計均數的非校正多重比較。
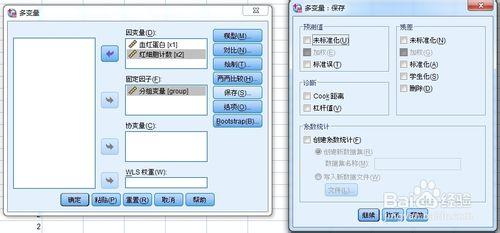
“輸出”:描述統計、SSCP矩陣、方差齊性檢驗。
結果解釋:
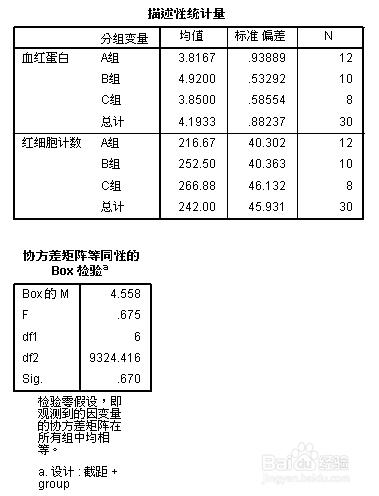
對統計量的基本描述;對協方差等同性檢驗的概率為0.670,大於顯著性水平0.05,協方差陣齊性,適合做多元方差分析。
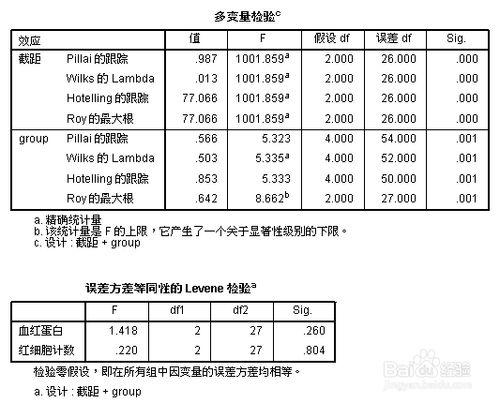
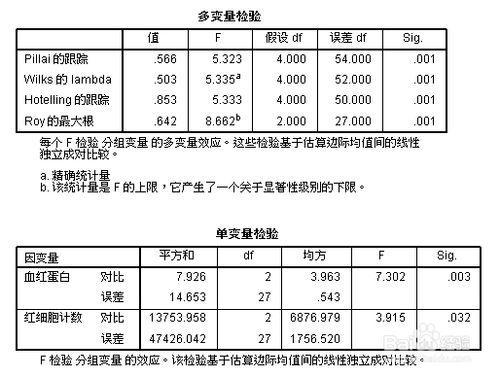
“多變量檢驗”:四種多元方差分析方法,Wilks' Lambda檢驗具有簡單的優點,並且與似然比準則有關,觀察三組均向量間有顯著差異,概率為0.001,可進一步兩兩比較;但是該過程不能作均向量兩兩比較。
“誤差方差等同性檢驗”:計算出的概率分別是0.260、0.804,都大於顯著性水平0.05,所以接受原假設。
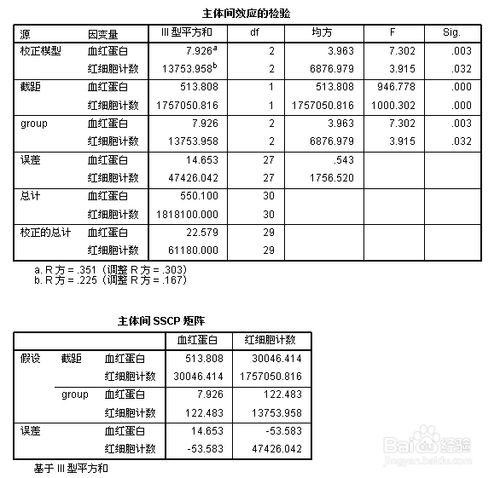
單變量組間比較的方差分析,由“校正模型”知,三組血紅蛋白間比較有顯著差異,概率為0.003,紅細胞概率為0.032,有顯著差異。
“主體間SSCP矩陣”:結果見圖片,具體解釋參考相關書籍。方差-協方差矩陣的分解。
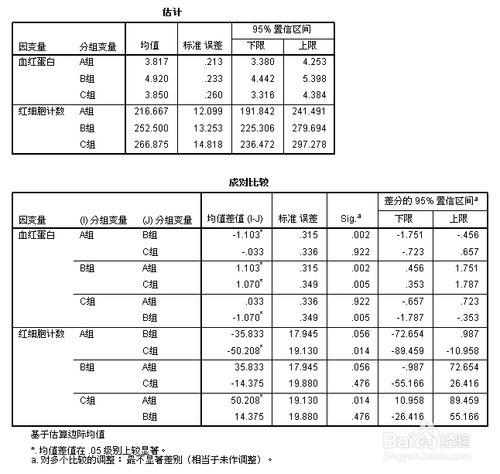
“估計”是單變量多重比較的基本統計量。
“成對比較”是LSD多重比較結果,單變量多重比較,對於血紅蛋白,B組最高,C組其次,A組最後。紅細胞計數的結果也是B組最高,C組其次,A組最後。