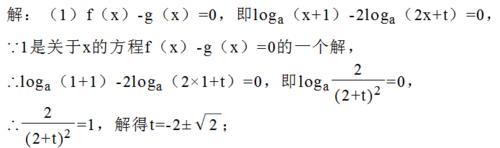61.已知0<a<1,函式f(x)=loga(x+1),g(x)=2loga(2x+t)(t∈R).(1)若1是關於x的方程f(x)-g(x)=0的一個解,求t的值;(2)當t=-1時,解不等式f(x)≤g(x);(3)若函式F(x)=af(x)+tx2+2t+1在區間(-1,2]上有零點,求t的取值範圍.
方法/步驟
(1)由f(1)-g(1)=0,即可求得t的值;(2)當t=-1時,f(x)≤g(x)即loga(x+1)≤2loga(2x-1),利用對數函式的單調性可得真數間的大小關係,注意對數函式的定義域;(3)分情況討論:當F(x)的零點為2時,可得F(2)=0求得t值;當F(x)在(-1,2)內有零點時,根據函式零點判定定理可得不等式,解出即可;
(1)由f(1)-g(1)=0,即可求得t的值;
(1)f(x)-g(x)=0,即loga(x+1)-2loga(2x+t)=0,∵1是關於x的方程f(x)-g(x)=0的一個解,∴loga(1+1)-2loga(2×1+t)=0,
即loga2(2+t)2=0,
∴2(2+t)2=1,
解得t=-2±√2;
(2)當t=-1時,f(x)≤g(x)即loga(x+1)≤2loga(2x-1),利用對數函式的單調性可得真數間的大小關係,注意對數函式的定義域;
(2)當t=-1時,f(x)≤g(x)即loga(x+1)≤2loga(2x-1),也即loga(x+1)≤loga(2x-1)2,又0<a<1,則x+1≥(2x-1)2①,且x+1>0②,2x-1>0③,聯立①②③,解得12<x<≤54,
∴不等式f(x)≤g(x)的解集為:(12,54];
(3)分情況討論:當F(x)的零點為2時,可得F(2)=0求得t值;當F(x)在(-1,2)內有零點時,根據函式零點判定定理可得不等式,解出即可;
(3)F(x)=af(x)+tx2+2t+1=aloga(x+1)+tx2+2t+1=x+1+tx2+2t+1=tx2+x+2t+2,若x=2是F(x)的零點,則有F(2)=0,即4t+2+2t+2=0,6t+4=0,解得t=-23;
若F(x)在(-1,2)內有零點,則有F(-1)F(2)<0,即(t-1+2t+2)(4t+2+2t+2)<0,整理得(3t+1)(6t+4)<0,解得-23<t<-13
綜上所述,-23≤t<-13,
故要使函式F(x)=af(x)+tx2+2t+1在區間(-1,2]上有零點,t的取值範圍為:-23≤t<-13.
注意事項
本題考查函式零點判定定理、對數不等式的解法,屬中檔題,解對數不等式要注意考慮對數函式定義域.