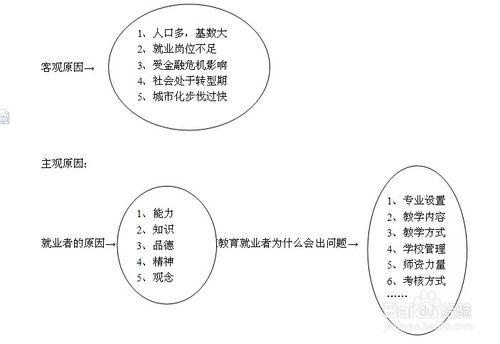
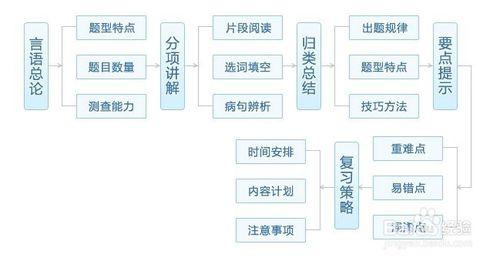
數學運算主要考查考生理解、把握事物間量化關係和解決數量關係問題的能力,主要涉及數據關係的分析、推理、判斷、運算等。該部分是國家公務員考試中大多數考生耗費時間長、正確率低的一個部分,總體難度相對較大。
本章將重點介紹數學運算幾種重要的解題技巧,幫助考生快速準確解題。
工具/原料
公務員複習資料、書籍、真題
草稿紙,筆等
方法/步驟
特值法:所謂特值法,就是在某一範圍內取一個特殊值,將繁雜的問題簡單化,這對於只需要把握整體分析的數學運算題非常有效。其中“有效設‘1’法”是最常用的特值法。
例題:某村的一塊試驗田,去年種植普通水稻,今年該試驗田的1/3種上超級水稻,收割時發現該試驗田的水稻總產量是去年總產量的1.5倍。如果普通水稻的產量不變,則超級水稻的平均產量與普通水稻的平均產量之比是:
A.5:2 B.4:3 C.3:1 D.2:1
技巧分析:取特殊值。設普通水稻的產量是1,則去年的總產量是1,今年的總產量就是1.5,今年普通水稻產量為2/3,超級水稻產量為1.5-2/3,而超級水稻只佔1/3,所以如果都種超級水稻的產量就是3×(1.5-2/3),那麼超級水稻的平均產量與普通水稻的平均產量之比是3×(1.5-2/3):1=2.5:1=5:2。故答案為A。
分合法:分合法主要包括分類討論法和分步討論法兩種,重點應用於排列組合問題中。在解答某些數學運算問題時,會遇到多種情況,需要對各種情況加以分類,並逐類求解,然後綜合得解,這就是分類討論法。而分步討論法則是指有時候有些問題我們一步是無法解決的,此時需要把問題進行分步,按步驟一步一步地解決。
例題:有一批長度分別為3、4、5、6和7釐米的細木條,它們的數量足夠多,從中適當選取3根木條作為三角形的三條邊,可能圍成多少個不同的三角形?A.25個 B.28個 C.30個 D.32個
技巧分析:分情況討論,(1)等邊三角形,有5種;(2)等腰三角形,3為腰時,4,5可為底;4為腰時,3,5,6,7可為底;5為腰時,3,4,6,7可為底;6為腰時,3,4,5,7可為底;7為腰時,3,4,5,6可為底。(3)三邊互不相等時,3,4,7不能構成三角形,共有-1=9種。綜上所述,共有5+2+4+4+4+4+9=32個。故答案為D。
比例法
根據題幹中相關比例數據,解題過程中將各部分份數正確畫出來,進行分析,往往能簡化難題,加速解題。
例題:甲、乙兩班學生到離學校24千米的飛機場參觀。但只有一輛汽車,一次只能乘坐一個班的學生,為了儘快到達飛機場,兩個班商定,由甲班先坐車,乙班先步行,同時出發,甲班學生在途中某次下車後再步行去飛機場,汽車則從某地立即返回接在途中步行的乙班學生,如果兩班學生步行的速度相同,汽車速度是他們步行速度的7倍,那麼汽車在距飛機場多少千米處返回接乙班學生,才能使兩班學生同時到達飛機場?
A.1.5 B.2.4 C.3.6 D.4.8
技巧分析:甲先坐車,乙走路,當汽車把甲班送到C點,甲班學生下車走路,汽車返回在B點處接乙班的學生,根據時間一定,路程的比就等於速度的比: 簡單化下圖:
時間一定,路程比等於速度比。所以乙走的路程AB比上車走的路程AB+2BC(因為是到了C點再回到B點,所以是2BC)
即AB:AB+2BC=1:7 ,AB:2BC=1:6 ,AB:BC=1:3
同理BC:CD=3:1 ,所以AB:BC:CD=1:3:1
題目問的是“那麼汽車在距飛機場多少千米處返回接乙班學生,才能使兩班學生同時到達飛機場”,很明顯是求CD段的長度,全程是5份,CD佔1份 。所以CD=24/5*1=4.8。故答案為D。
尾數計算法
尾數法是數學運算題解答的一個重要方法,即當四個答案全不相同時,我們可以採用尾數計算法,最後選擇出正確答案。
例題:3×999+8×99+4×9+8+7的值是( )
A.3840 B.3855 C.3866 D.3877
技巧解析:運用尾數法。尾數和為7+2+6+8+7=30,尾數為0。故答案為A。
計算代換法
計算代換法是指解數學運算題時,把某個式子看成一個整體,用一個變量去代替它,從而使問題得到簡化。實質是數量之間的轉化,目的是變換研究對象,將問題移至新對象的知識背景中去研究,從而使非標準型問題標準化、複雜問題簡單化,變得容易處理。
例題:計算(1+0.23+0.34)×(0.23+0.34+0.65)-(1+0.23+0.34+0.65)×(0.23+0.34)值。
技巧分析:數量代換為,0.23+0.34=A,0.23+0.34+0.65=B那麼原式應為(1+A)*B-(1+B)*A=B-A=0.65。通過數量代換,可以使得計算達到事半功倍的效果。
注意事項
熟悉簡單題目,基本功很重要。
化解較難題目,技巧十分關鍵。