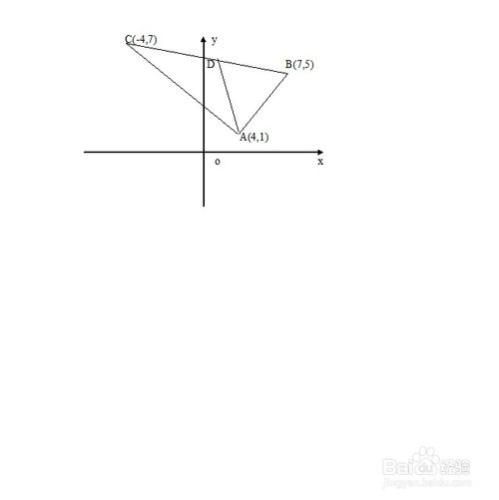
在△ABC中,A(4,1),B(7,5),C(-4,7),用三種方法求∠A的平分線的方程。
工具/原料
知識點一:角平分線定理及兩點距離公式
知識點二:到角知識應用
知識點三:向量知識的應用
方法/步驟1:角平分線定理及兩點距離公式
[解題思路]:因為是角平分線,利用角平線定理即兩點間距離公式來求點D,進而求其方程。
根據兩點間距離公式得到:
AC=√[(4+4)^2+(1-7)^2]=10;
AB=√[(7-4)^2+(5-1)^2]=5;
BC=√[(-4-7)^2+(7-5)^2]=5√5.
設CD=x,則BD=5√5-x。
根據角平分線定理得到:
BD/DC=AB/AC
所以:
(5√5-x)/x=5/10,得到:x=10√5/3,則CD=10√5/3,BD=5√5/3.
設D(m,n),因為D在直線BC上,則有:
(n-5)/(m-7)=(5-7)/[7-(-4)],即:
11n+2m-69=0
2m=69-11n……(1)
CD^2=x^2=500/9=(m+4)^2+(n-7)^2…..(2)
BD^2=125/9=(m-7)^2+(n-5)^2…..(3)
(3)-(2)得到:
375/9=8m+14m-14n+10n+16+49-49-25
化簡:22m-4n-9=375/9
將(1)代入上式得到:
11(69-n)-4n-9=375/9
750-125n=375/9
125(6-n)=125*3/9
所以n=17/3,進一步得到m=10/3. 即D(10/3,17/3).
則AD的斜率k=(17/3-1)/(10/3-4)=-7.
所以角平分線的方程為:
y-1=-7(x-4)
即:7x+y-29=0.
方法/步驟2:到角知識應用
[解題思路]:利用到角公式求出所求直線的斜率,直線經過A點,用點斜式即可得到直線方程。
直線AC的斜率k1=(7-1)/(-4-4)=-3/4
直線AB的斜率k2=(5-1)/(7-4)=4/3.
設∠CAD=∠DAB=∠a,角平分線的斜率=k,由到角公式得到:
(k-k2)/(1+k2·k)=(k1-k)/(1+k1·k)
代入數值得到:
(k-4/3)/(1+4k/3)=(-3/4-k)/(1-3k/4)
化簡得到:
(3k-4)^2=(4k+3)^2
得到:k=-7或者k=-1/7,
因為k
點斜式得到角平分線方程為:
y-1=(-7)(x-4)
即:7x+y-29=0.
方法/步驟3:向量知識的應用
[解題思路]:利用向量點乘的有關知識進行求解。
設D(m,n),因為D在直線BC上,則有:
(n-5)/(m-7)=(5-7)/[7-(-4)],即:
11n+2m-69=0
2m=69-11n……(1)
向量AC=(-8,6),向量AD=(m-4,n-1),則:
向量AC·向量AD=-8(m-4)+6(n-1)
= AC * AD *cos∠CAD………(2)
向量AB=(3,4),向量AD=(m-4,n-1),則:
向量AB·向量AD=3(m-4)+4(n-1)
= AB * AD *cos∠DAB………(3)
(2)/(3)得到:
[-8(m-4)+6(n-1)]/[ 3(m-4)+4(n-1)]= AC / AB =2
所以:
n+7m=29………(4)
由(1)、(4)解方程得到:
m=10/3,進而得到n=17/3,即D(10/3,17/3).
則AD的斜率k=(17/3-1)/(10/3-4)=-7.
所以角平分線的方程為:
y-1=-7(x-4)
即:7x+y-29=0.
注意事項
在直線的斜率問題中,在豎直方向的左側,與豎直方向的夾角越小,其斜率也越小。
對於本題,角平分線的斜率小於直線AC的斜率。