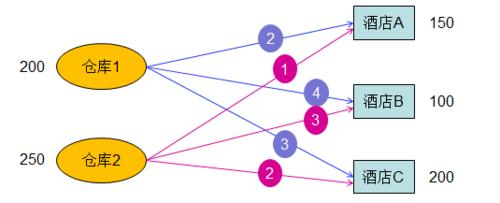
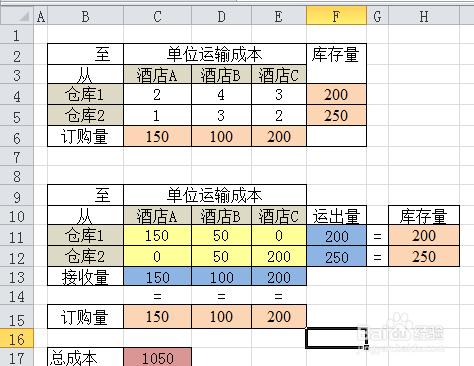
本文討論的是一個運輸問題,一個供貨商給3家酒店(酒店A、酒店B、酒店C)提供啤酒,該供應商在本市有2個倉庫,倉庫1、倉庫2,每個倉庫到3家酒店的運輸成本不同,每家酒店對啤酒的需求量不同,每個倉庫現存的啤酒箱數不同。
問該供應商如何安排兩個倉庫的發貨數量,在保證酒店需求的前提下,總運費最低。
工具/原料
Excel 2010
方法/步驟
(1)輸入已知條件
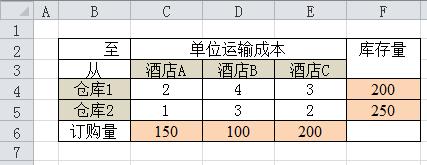
講問題的已知條件轉換為一個矩陣,在Excel中輸入。
C列表示酒店A的事;
D列表示酒店B的事;
E列表示酒店C的事;
第4行表示倉庫1的事;
第5行表示倉庫2的事;
於是,可以在【C4:E5】這個範圍輸入單位運輸成本。
-----------
F列表示庫存量的事;於是【F4】表示倉庫1的庫存、【F5】表示倉庫2的庫存
-----------
第6行表示需求量的事;於是【C6】表示酒店A的需求量、【D6】表示酒店B的需求量、【E6】表示酒店C的需求量.
(2)建立模型
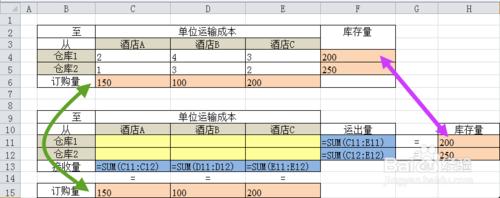
***複製區域【B2:E5】,選中單元格【B9】,粘貼。
***刪除【C11:E12】的數據,作為可變單元格(自變量)——表示運輸數量
***在單元格【F11】輸入函數【=SUM(C11:E11)】,選中單元格【F11】,拖拽至【F12】,則計算了兩個倉庫的運出數量
***在單元格【C13】輸入函數【=SUM(C11:C12)】,選中單元格【C13】,拖拽至【E13】,則計算了3個酒店的接收的數量
***複製【F4:F5】的內容到【H11:H12】,複製庫存量
***複製【C6:E6】的內容到【C15:E15】,複製需求量
***計算總運輸成本
在單元格【C17】輸入函數【=SUMPRODUCT(C4:E5,C11:E12)】
sumproduct函數包括兩個單詞,sum(求和)、product(乘法),所以意思“先乘,後求和”
本公式中區域【C4:E5】內的單元格與區域【C11:E12】內的單元格分別先乘後求和,就是運輸量乘以運輸成本,然後加總,所以是總的運輸成本。
(3)規劃求解
點擊【數據】——【規劃求解】
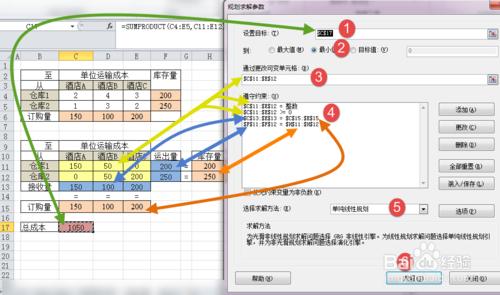
***在彈出的窗口,【設置目標】,點擊右側的按鈕,選中單元格【C17】——總運輸成本
***其下,點選【最小值】——想求最小的總運費
***其下,【可變單元格】點擊右側的按鈕,選中區域【C11: E12】——6個自變量
***在【規劃求解】窗口,點擊右側的【添加】,添加4類約束條件
其一、運出量 = 庫存量
其二、接收量 = 需求量
其三、自變量是整數
其四、自變量大於等於零
***求解方法,點選【單純線性規劃】
最優解是
倉庫1將150箱運往酒店A,50箱運往酒店B
倉庫2將50箱運往酒店B,200箱運往酒店C
總的運輸成本是1050元