函數的性質有哪些?

在高中文科數學中，函數始終是一個重點，同時也是一個難點。

如何學好函數，必不可少的就是了解並掌握函數的性質。

工具/原料

筆，紙

方法/步驟

性質一：對稱性

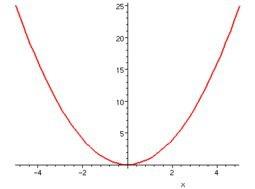
數軸對稱：所謂數軸對稱也就是說函數圖像關於座標軸X和Y軸對稱。

原點對稱：同樣，這樣的對稱是指圖像關於原點對稱，原點兩側，距離原點相同的函數上點的座標的座標值互為相反數。

關於一點對稱：這種類型和原點對稱頗為相近，不同的是此時對稱點不再僅限於原點，而是座標軸上的任意一點。

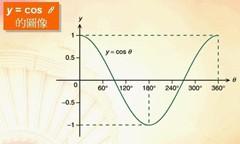
性質二：週期性

所謂週期性也就是說，函數在一部分區域內的圖像是重複出現的，假設一個函數F(X)是周期函數，那麼存在一個實數T，當定義域內的X都加上或者減去T的整數倍時，X所對應的Y不變，那麼可以說T是該函數的週期，如果T的絕對值達到最小，則稱之為最小週期。

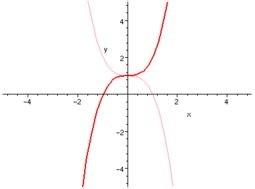
性質三：奇偶性

奇偶性是指函數關於原點還是Y軸對稱。

奇偶性成立的條件是定義域關於原點對稱，如果定義域為[-1，9]，那麼就沒有必要考慮奇偶性，直接就可以定義為非奇非偶函數。

在這個前提下，如果F(-X)=F(X)則為偶函數，如果F(-X)=-F(X)則為奇函數。

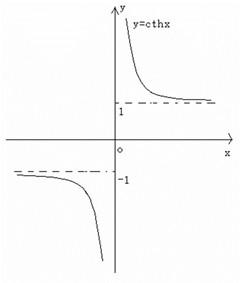
性質四：單調性

這一性質是在函數運算中運用最為廣泛的

它的主要用途在於計算函數定義域，值域，和最大最小值。

如何計算極值：最直觀的方法是看圖，在學習到導數時，變幻的不等式將講解其他做法。

注意事項

本經驗由變幻的不等式撰寫

如果您覺得本經驗對您有一定幫助不妨投出您寶貴的一票