在進行數據分析的時候我們有時候需要求我們建立的矩陣的特徵值,尤其是最大特徵值以及其對應的特徵向量。小編還記得當初學習矩陣的時候筆算特徵值和特徵向量的痛苦,隨著矩陣階數的擴大,運算量比較大,但是如果使用軟件Matlab來計算可以節省很多時間。所以今天小編和大家一起使用Matlab來計算矩陣的最大特徵值和相應的特徵向量
工具/原料
Matlab R2012a
電腦
方法/步驟
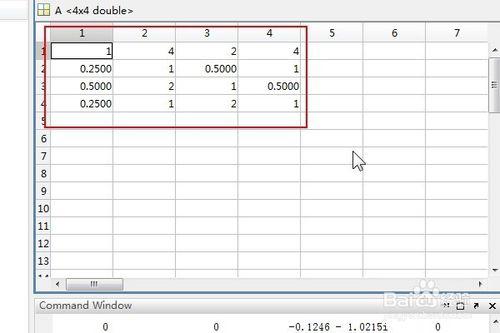
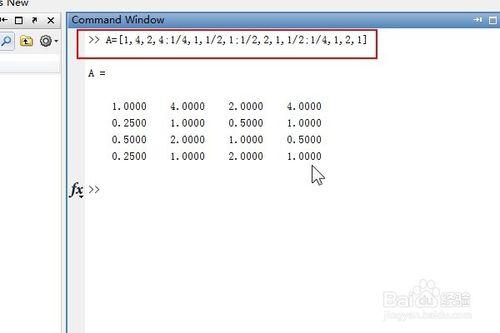
啟動Matlab ,在命令窗口輸入要處理的矩陣A
A=[1,4,2,4;1/4,1,1/2,1;1/2,2,1,1/2;1/4,1,2,1]
輸入完成後回車軟件會按行列的形式顯示矩陣
順便我們可以檢查一下矩陣是否輸入錯誤
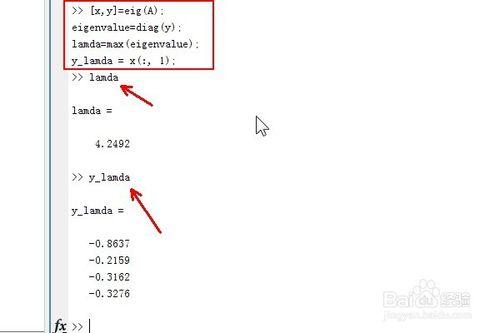
接著輸入[x,y]=eig(A) 回車
我們就可以看到矩陣的所有特徵值和特徵向量了
特徵值是對角矩陣y 矩陣x的每一列對應一個y中相應列的特徵值
此處注意括號必須是在英文輸入法下輸入 如果顯示紅色表示有問題需要重新輸入
雖然我們已經計算出了矩陣的特徵值和特徵向量 但是如果我們只是計算這一個的話 我們完全可以觀察得到最大的特徵值
接著輸入
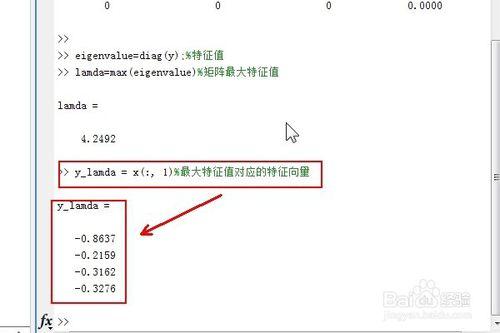
eigenvalue=diag(y);
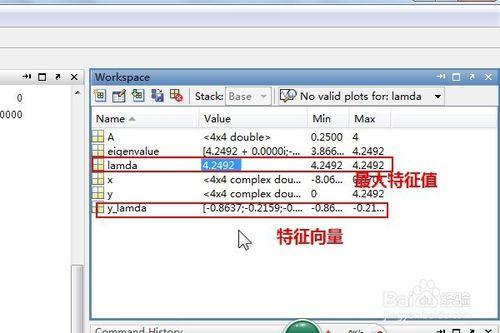
lamda=eigenvalue(1)
lamda表示最大的特徵值 這裡lamda=4.2498
求出矩陣最大特徵值之後我們雖然可以一眼看到特徵向量 但是不方便以後我們大量的處理矩陣
此時再輸入
y_lamda = x(:, 1) 即最大特徵值對應的特徵向量
上面的過程只是適合我們進行一次兩次這樣的計算 如果遇到需要較多的矩陣的時候或者這樣的過程只是某些計算中的幾步需求的時候我們就需要把前面的計算合在一起進行計算 比如小編這樣 同樣我們也可以把這段代碼放在需要的算法程序中
除了直接輸入變量結果來查看的方法外 我們還可以直接在workspace中查看變量運算結果 如圖中的lamda和y_lamda的結果值
注意事項
經驗系小編獨立創作完成,如果您有更好的方法,請不吝賜教!