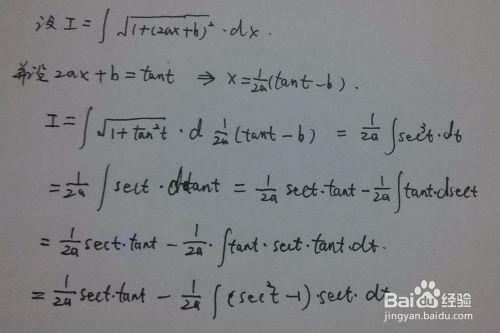積分求拋物線線段的長度,本經驗介紹用定積分的方法,求解一段拋物線y=ax^2+bx+c曲線的長度的方法。主要是通過弧長積分,即ds=√(1+y'^2)dx。
工具/原料
曲線的弧度積分方法。
不定積分的求導方法
1.基本公式表達
本例子介紹拋物線y=ax^2+bx+c,在一段區間上的曲線長度的積分表示。
√[1+(2ax+b)^2的不定積分求解過程。
在積分過程中出現於被積函數同樣的情形,即:
I=g(x)-I+f(x)
則:
2I=g(x)+f(x)
得到:
l=(1/2)[g(x)+f(x)].
通過換元后,最終表達式必須回代原積分變量。
2.介紹以y軸為對稱軸的情形
3.介紹對稱軸為y=k情形
注意事項
弧度積分的座標表示ds=√(1+y'^2)。