現在條件好了,寶寶的成長過程中,有的是好吃的、好穿的,缺少的就是“優質教育”,而優質教育中,智力開發是很重很重的一筆。
如果有一個“牽引智慧的帆”,我相信家長們都會爭相購買。其實它就在我們身邊,也並不太難,就是大家常說的“思維訓練”。
今天順手把過去給我寶寶用過的“思維訓練”分享給大家。有找規律填數題、算式推導題和邏輯思維題,指望著舉一反三,找出最適合你家孩子的開發途徑,讓祖國的花朵自然開放! ——陡勢橫橋
一、三角填數
三個三角有個空
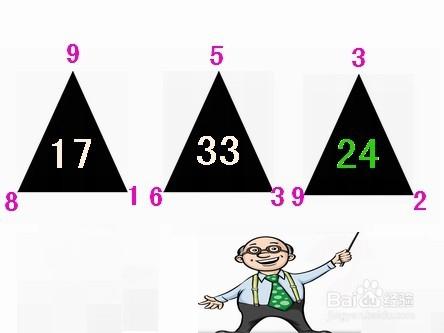
如圖,三個三角形,周圍都有數字;三角形中間也有數字,就是最右邊的沒有,需要你填上。
當然,外邊的數字和中間的數字肯定有點關係,請你把它們的規律找出來,再計算出“?”處應該是個什麼數。你能做到嗎?
填空計算
看出來了嗎?別急,先找找規律。三角形三個角的三個數,與三角形中間的數,是有數字關係的……
突然,你可能眼睛一亮,看出了規律:
三角形中間的數,等於上角數加上左下角數,再與右下角數相乘。即:
三角形中間的數=(上角數+左下角數)×右下角數
“?”=(3+9)×2=24
二、補全算式
殘缺的算式
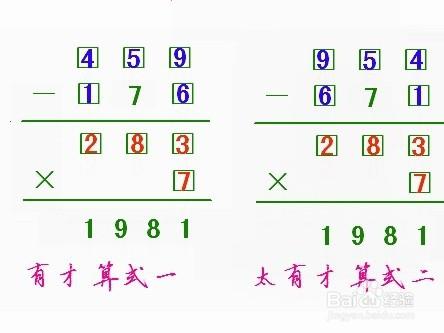
如圖,是個殘缺的算式,你需要好好動動腦筋,把1、2、3、4、5、6、7、8、9這九個數分別填入“□”小方框中,使算式成立。
起步艱難
我們只知道得數是“1981”,所以先要從乘法部分推導。
看“1981”的尾數是1,乘法中只有9×9和3×7的尾數能得到“1”,9×9要用兩個9,和題意不符,故取3×7。如圖,3放下面為乘數,7為被乘數的尾數。
進一步,三、七得二十一後,寫1,進2,要和“1981”的“8”對上,還需要個“6”,所以被乘數中間的數字只能是2,二、三得六,加二得八,推導順利。
可是,再往下就不行了,什麼數乘以3能得19呀?推演到此止步,如圖。
重捋思路
開始的思路是對的,是不是“3”和“7”的位置搞錯了。如圖,調整為7為乘數,3為被乘數的尾數。
同樣是三、七得二十一,寫1,進2,“7”和什麼數相乘尾數是“6”?只有8。所以被乘數中間的數字填寫8,被乘數前面的數字填寫2(只能填2)。仔細看一遍,乘法部分推導成功了!如圖。
縝密思維
相對而言,減法部分就容易一些。現在我們知道,還有剩下的1、4、5、6、9五個數,還知道減法部分的得數“差”是“283”。要使這個“差”的個位是3的,只能有9-6和4-1兩種可能,我們分別試一試:
①在“被減數”的個位填寫9,“減數”的個位填寫6。再推導“被減數”的中間數字。什麼數減7等於8?當然是15,這就確定了“被減數”中間數字是5,剩下的4和1就好辦了,4填寫在上面,1填寫在下面,檢查一遍,成功了,如圖。
②換一換,看看能否可行。
“被減數”的個位填寫4,“減數”的個位填寫1。“被減數”中間數字還是填5,剩下的9和6分別填寫在上面和下面,檢查一遍,也成功了,如圖。
即本題有兩種填法,太有才了。
三、警察斷事
事出有因
甲、乙、丙三個要好的同學放學一起回家。在途中撿到一塊手錶,就交給了執勤的警察。警察問他們三人是誰最先發現的手錶。三個機靈的小朋友這樣表述。
甲說:“不是我發現的,也不是乙。”
乙說:“不是我,也不是丙。”
丙說:“不是我,我也不知道是誰發現的。”
三個小朋友又告訴警察,他們每個人說的兩句話中,都有一句是真的,一句是假的。
這個年青的警察很聰明,馬上就指出了發現手錶的小朋友。
給你10分鐘,能推斷是誰發現的手錶嗎?
警察神斷
警察根據每個人的話中,一句是真,一句是假,很容易推斷出結果,思路如下:
三個同學一起回家,自然發生的事情都知道。丙同學的第二句話,說他不知道是誰發現的,肯定是假話,那麼,丙同學的第一句話,就是真的。也就是說丙同學不是首先發生手錶的人。
這樣,乙同學“不是我,也不是丙”的話中,後半是真的,那麼前面的“不是我”是假的,所以,首先發現手錶的是同學乙。
你是這樣思考的嗎?