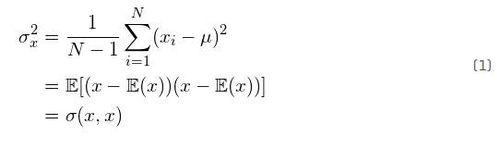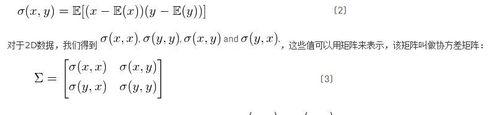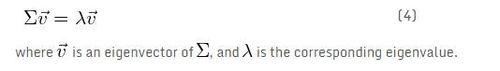本文中,我們通過探索線性變換與所得資料協方差之間的關係提供協方差矩陣一個直觀的幾何解釋。大部分教科書基於協方差矩陣的概念解釋資料的形狀。相反,我們採取一個反向的方法,根據資料的形狀來解釋協方差矩陣的概念。
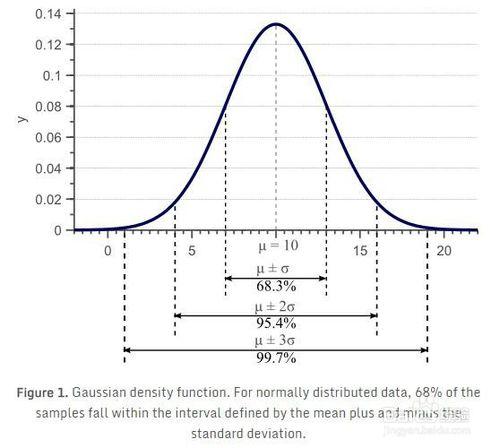
在文章中,我們會討論方差的概念,並提供了眾所周知的估算樣本方差公式的推導和證明。這篇文章中使用的圖1表明標準差(方差的平方根)提供了資料在特徵空間上傳播多少的量度。
方法/步驟
我們發現,樣本方差的無偏估計可由下式獲得:
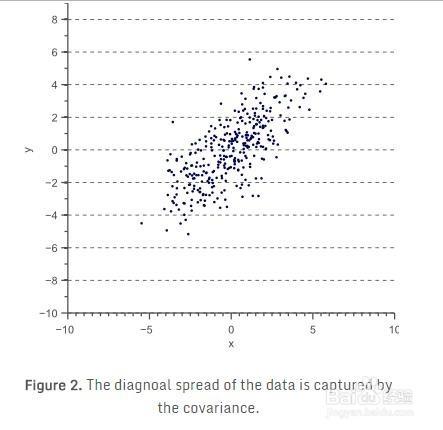
然而,方差只能用於解釋平行於特徵空間軸方向的資料傳播。考慮圖2所示的二維特徵空間:
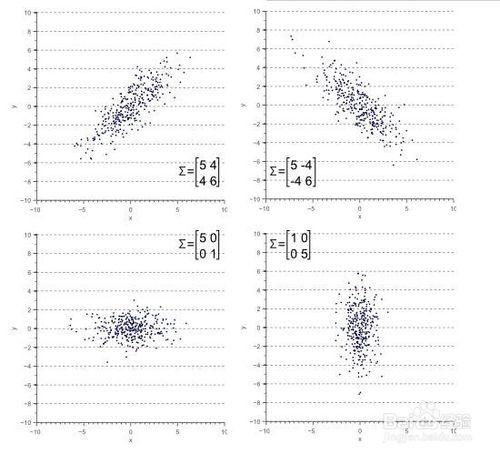
對於這個資料,我們可以計算出在x方向上的方差和y方向上的方差。然而,資料的水平傳播和垂直傳播不能解釋明顯的對角線關係。圖2清楚地顯示,平均而言,如果一個數據點的x值增加,則y值也將增加,這產生了正相關。這種相關性可以通過擴充套件方差概念到所謂的資料“協方差”捕捉到:
如果x與y是正相關的,那麼y和x也是正相關的。換句話說,。因此,協方差矩陣始終是一個對稱矩陣,其對角線上是方差,非對角線上是協方差。二維正態分佈資料由它的均值和2x2協方差矩陣就可以完全解釋。同樣,一個3x3協方差矩陣用於捕捉三維資料的傳播,一個NxN協方差矩陣捕獲N維資料的傳播。
圖3展示了資料的整體形狀如何定義協方差矩陣:
協方差矩陣的特徵值分解
在下一節,我們將討論協方差矩陣如何被解釋為白色資料轉換成我們觀察到資料的線性操作。然而,在深入技術細節之前,對特徵向量和特徵值如何唯一地確定協方差矩陣(資料形狀)有一個直觀的認識是非常重要的。
正如我們在圖3看到的,協方差矩陣定義了我們資料的傳播(方差)和方向(協方差)。因此,如果我們想用一個向量和它的大小來表示協方差矩陣,我們應該簡單地嘗試找到指向資料最大傳播方向上的向量,其大小等於這個方向上的傳播(方差)。
如果我們定義這個向量為,那麼我們資料D到這個向量上的對映為,對映資料的方差是。由於我們正在尋找指向最大方差方向的向量,所以我們應該選擇它的成分,使得對映資料的協方差矩陣儘可能的大。最大化的形式為的任何函式,其中是歸一化單位向量,可以用一個所謂的瑞利商表示。通過設定等於矩陣的最大特徵特徵向量可以獲得這樣瑞利商的最大值。
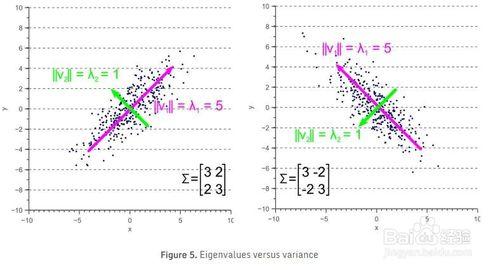
換句話說,協方差矩陣的最大特徵向量總是指向資料最大方差的方向,並且該向量的幅度等於相應的特徵值。第二大特徵向量總是正交於最大特徵向量,並指向第二大資料的傳播方向。
現在,讓我們來看看一些例子。在文章《特徵值和特徵向量》中我們看到一個線性變換矩陣T完全由它的特徵向量和特徵值定義。應用到協方差矩陣,這意味著:
如果我們資料的協方差矩陣是對角矩陣,使得協方差是零,那麼這意味著方差必須等於特徵值λ。如圖4所示,特徵向量用綠色和品紅色表示,特徵值顯然等於協方差矩陣的方差分量。
然而,如果協方差矩陣不是對角的,使得協方差不為零,那麼情況稍微更復雜一些。特徵值仍代表資料最大傳播方向的方差大小,協方差矩陣的方差分量仍然表示x軸和y軸方向上的方差大小。但是,因為資料不是軸對齊的,所以這些值不再與圖5所示的相同。
通過比較圖5與圖4,可以清楚地看到特徵值表示沿特徵向量方向資料的方差,而協方差矩陣的方差分量表示沿軸的傳播。如果沒有協方差,則這兩個值是相等的。
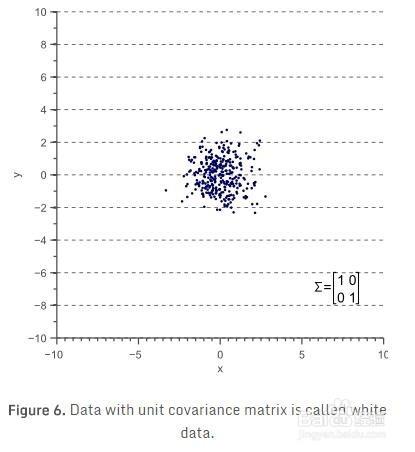
圖6所示的資料是D
在下面的段落中,我們將討論協方差矩陣與線性變換矩陣T= RS之間的關係。
讓我們先從未縮放(縮放相當於1)和未旋轉的資料開始。在統計中,這往往為“白資料’,因為它的樣本是從標準正態分佈引出的,因此對應於白(不相關)噪聲: