本文介紹使用Excel的規劃求解模塊解決一個簡單的管理科學應用問題。
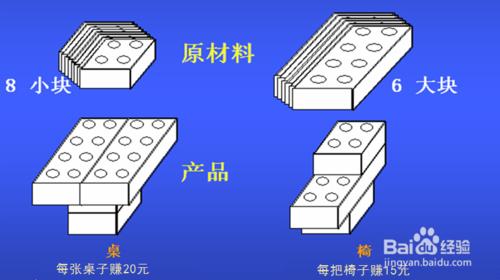
每個小組都有8個小木塊和6 大木塊用於拼裝桌子和椅子;
每張桌子可以賺20元,每把椅子可以賺15元;
每張桌子用2個小木塊和2 大木塊;
每張桌子用2個小木塊和1 大木塊;
問組裝幾張桌子,幾把椅子,賺錢最多?
0 信息應用01: 加載Excel的規劃求解模塊
工具/原料
Excel 2010
方法/步驟
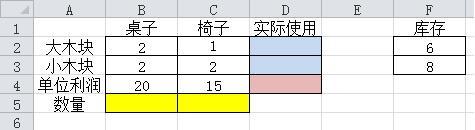
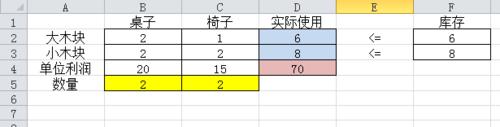
(1)輸入已知條件
Exce軟件的結構是行和列。
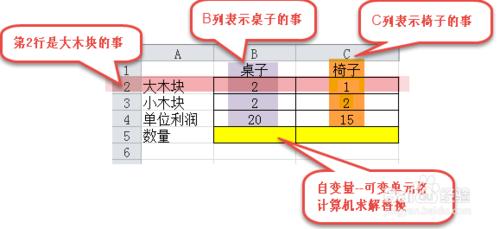
B列表是桌子的事,C列表示椅子的事
第2行表示大木塊的事
那麼單元格【B2】就表示每張桌子用幾個大木塊,輸入已知條件2
第3行表示小木塊的事
第4行表示單位利潤的事
第5行表示數量的事
於是,B5、C5就是決策變量(自變量,可變單元格)——計算機會求解替換其取值。
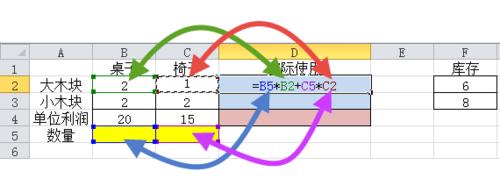
(2)輸入函數
在單元格【D2】輸入函數【=B5*B2+C5*C2】
在單元格【D3】輸入函數【=B5*B3+C5*C3】
在單元格【D4】輸入函數【=B5*B4+C5*C4】
---------補充說明
較為一般的方法是,在在單元格【D2】輸入函數【=$B$5*B2+$C$5*C2】
因為自變量【$B$5】和【$C$5】總要用,所以是絕對引用
然後選中單元格【D2】,拖拽生成3個函數
--------
更一般的方法是,在在單元格【D2】輸入函數【=sumproduct($B$5:$C$5, B2:C2)】
因為自變量【$B$5:$C$5】總要用,所以是絕對引用
這種方法的好處是處理大模型——比如10行8列的模型更有效率
0 Excel基礎02:相對引用、絕對引用與混合引用
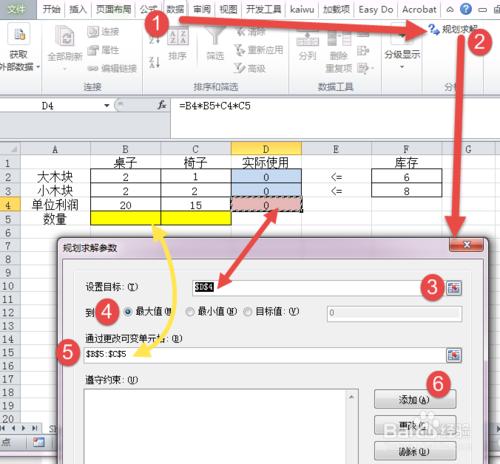
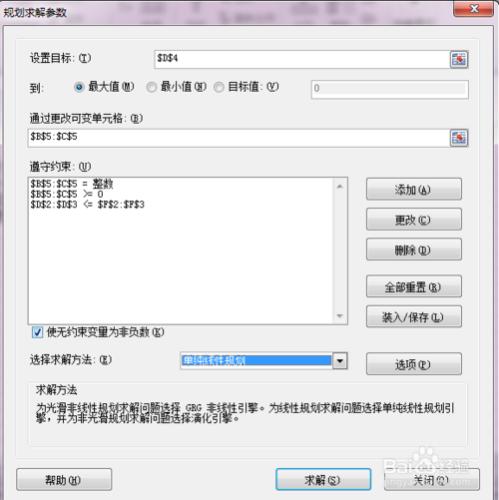
(3)設置規劃求解模塊
***點擊【數據】——【規劃求解】
***在彈出的窗口,【設置目標】,點擊右側的按鈕,選中單元格【D4】——總利潤
***其下,點選【最大值】——想求最大的總利潤
***其下,【可變單元格】點擊右側的按鈕,選中區域【B5:C5】——兩個自變量
0 信息應用01: 加載Excel的規劃求解模塊
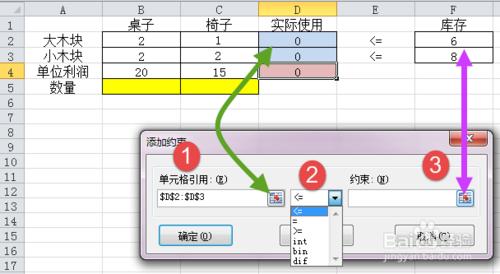
(4)添加約束條件
在【規劃求解】窗口,點擊右側的【添加】,添加3類約束條件
其一、實際使用量<=庫存量
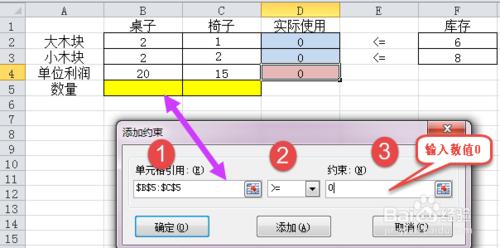
其二、自變量(桌子、椅子數量的數量)>=0
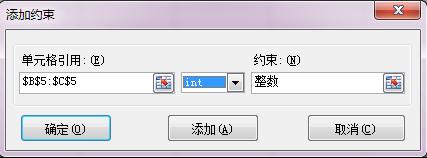
其三、自變量(桌子、椅子數量的數量)是整數
設置完成,點擊【求解】,就可以計算出最優解