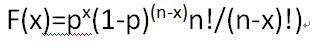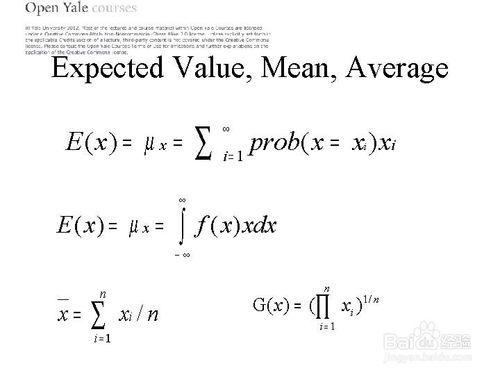本課介紹了課程中所有需要用到的數學知識。
方法/步驟
金融的基礎核心是概率論,概率用來描述某一事件發生的可能性。比如股市上漲的概率,火災發生的概率。
獨立事件,每次試驗和試驗的結果沒有關係。兩個獨立事件同時發生的概率:
p(a and b)=pa*pb
二項分佈(binomial distribution)N次試驗中發生x次的概率。比如10000個投保火災險中發生3次火宅次數的概率。這樣就可以算出可設置的合理保費。
均值,在一組數據中所有數據之和再除以這組數據的個數
期望值,uX=每個變量值x和對應概率的乘積的求和,適用於離散數值。
樣本均值,所有樣本之和除以樣本數。
幾何平均,所有樣本相乘的1/n次方(n為樣本數,樣本不能為負,不然結果為虛數)。幾何平均用來計算平均收益率更能反映實際盈利情況,但是因為通常比算術平均小,所以金融界通常不採用。
方差,標準差(方差開平方根),總體方差,樣本方差。
協方差,衡量兩個變量變動關係。正值為同向變動,負值為異向變動。
相關性,協方差除以各自方差,結果在-1到1之間。
效用方程,幸福度和所擁有的錢的數量呈邊際遞減。