在執行MATLAB程式設計進行資料的處理過程當中,我們常常用到matlab曲線擬合,但是工具箱由於需要人工互動,得到的擬合結果,需要人工的去提取,再輸入,所以,工具箱擬合結果十分不適合呼叫,以及繼續下面的操作,所以我們需要用到matlab曲線擬合函式,並且以最常用的多項式擬合函式為例作為matlab曲線擬合例子,進行詳細介紹。
工具/原料
MATLAB
matlab曲線擬合
資料準備:
關於MATLAB曲線擬合,我寫了一系列的經驗,為了相互統一,採用下面的資料:
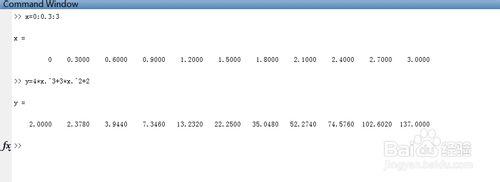
x=[0 0.3000 0.6000 0.9000 1.2000 1.5000 1.8000 2.1000 2.4000 2.7000 3.0000]
y=[2.0000 2.3780 3.9440 7.3460 13.2320 22.2500 35.0480 52.2740 74.5760 102.6020 137.0000]
由函式y=4*x^3+3*x^2+2 產生。
函式命令擬合:
MATLAB為我們提供了多項式擬合函式命令polyfit,下面我們就用這個函式命令進行擬合。
在MATLAB主視窗中輸入
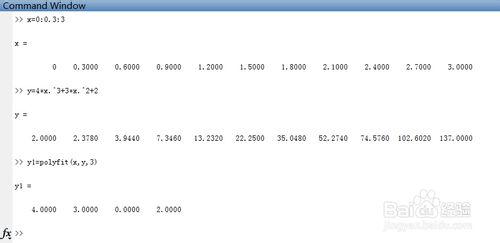
y1=polyfit(x,y,3),回車
我們會看到下面結果:
y1 =
4.0000 3.0000 0.0000 2.0000
函式的說明:
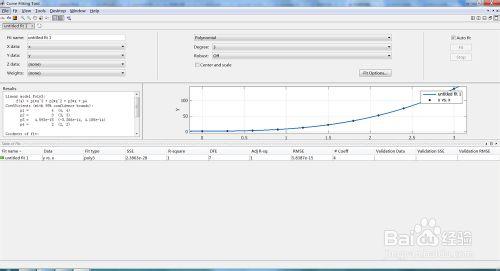
y1=polyfit(x,y,N),這裡函式polyfit第一個引數傳遞的是擬合數據的自變數,第二個引數是因變數,第三個引數是擬合多項式的階數,這個由我們給定。如下圖。我們可以給定不同的N,運用不同的多項式進行擬合。
輸出結果:
在上面的例子中我們看到輸出的結果是:
y1 =
4.0000 3.0000 0.0000 2.0000
對照原始的函式y=4*x^3+3*x^2+2 ,我們可以看到,y1其實輸出的是擬合函式的係數,並且由高次到低次由左到右輸出。
多項式階數N的確定:
這裡有些人可能會有問題了,我們事先不知道要擬合的資料是幾階的,那麼我們如何判斷我們給定的擬合階數N最終為多少呢?
階數確定方法一:
這種方法是最常用的確定方法,一般情況下,我們擬合函式的目的,就是為了呼叫,所以在用函式擬合之前會用matlab曲線擬合工具箱進行擬合函式階數的確定,由其確定擬合的階數,然後我們用這個函式命令在其他地方進行十分方便地呼叫,這是最常用的做法。我們往往擬合的是多個同類型的資料,所以確定好一組樣本的次數之後,就可以對其他資料用同樣的N進行擬合。
階數確定方法二:
這種方法方法可以取代用cftool進行判斷的過程,具體實現程式碼如下:
for i=1:5
y2=polyfit(x,y,i);
Y=polyval(y2,x);%計算擬合函式在x處的值。
if sum((Y-y).^2)<0.1
c=i
break;
end
end
執行以上程式,結果如下:
c=3
假設我們的誤差平方和精度範圍為0.1,那麼通過以上程式,我們可以看到用3階函式擬合,就可以達到精度要求。在多項式進行擬合的時候這個值我們在程式執行的過程中就直接可以呼叫。
說明:至於說用plot函式進行畫圖,肉眼觀察擬合程度的那種笨方法,我們不推薦,這裡也不贅述。
matlab曲線擬合結果呼叫及顯示
大家可能有疑問,我們擬合完函式之後得到的是擬合多項式的係數,我們應該如何呼叫?如何檢視我們擬合的多項式是什麼形式呢?下面我們就接著上面的內容進行介紹。
擬合多項式的顯示:
在MATLAB主視窗中輸入
syms x f(x)
f(x)=poly2sym(y2,x)
我們會看到輸出如下結果:
f(x) =
4*x^3 + 3*x^2 + (5822273280258613*x)/1267650600228229401496703205376 + 2
這就是我們擬合出來的多項式。
這裡我們看到一次項的係數並不是0,這裡5822273280258613/1267650600228229401496703205376=4.5930e-15,這個數量級我們完全可以忽略,認為是0。
擬合結果的呼叫:
在MATLAB主視窗中輸入如下命令:
TEST=polyval(y2,x)
我們可以看到如下結果,如下圖。
函式polyval()的第一個引數為多項式的係數,第二個引數為要計算的自變數值。可以是向量或者矩陣。
注意事項
如果以上經驗有用,請點選下方的 有用按鈕支援我的工作,謝謝!