《圓的面積》教學簡介
課程內容:
我選的內容為《圓的面積》,主要內容以圓的面積的推導為主,這是北師大版六年級數學上冊第一單元的內容。選題意圖是因為面積推導比較抽象,涉及“化曲為直”的轉化思想,學生理解有困難。學生已經學習了平行四邊形、三角形和梯形的面積公式的轉化推理過程,本節課的教學也運用“化曲為直”的轉化思想,結合多媒體課件,讓學生掌握圓面積公式的推導過程。
教學特色:
採用課中講解、多媒體演示和學生的動手操作活動,讓學生自主探究圓的面積的推導。
教學亮點:
1.化靜為動,化曲為直。運用演示,學生操作,讓學生多種感官參與,通過觀察,比較、分析,發現轉化前後的區別與聯絡,讓學生推匯出圓的面積計算公式。這樣由現象到本質的引導,使學生親身經歷數學化的學習過程,學生思維在交流中碰撞,在碰撞中發散,在想象中得以提升。探索能力、分析問題和解決同題的能力得到了提高。
2.在探索過程中滲透極限的數學思想,潤物細無聲,為學生的終身學習服務。通過學習,讓學生進一步學會數學地思考和解決問題,在凸顯新的教學理念的同時,又增加了數學課堂的厚度。
工具/原料
製作相應的ppt
方法/步驟
《圓的面積》教學設計
——北師大版六年級上冊數學第一單元
一、教學目標:
知識技能:讓學生經歷操作、觀察、驗證、討論和歸納等數學活動的過程,探索並掌握圓的面積計算公式,能正確計算圓的面積,並能應用公式解決相關的簡單實際問題,構建數學模型。
數學思考與問題解決:讓學習進一步體會“轉化”的數學思想方法,感悟極限思想的價值,培養運用已有知識解決新問題的能力,增強空間觀念,發展數學思維。
情感態度:讓學生進一步體驗數學與生活的聯絡,感受用數學的方式解決實際問題的過程,提高學習數學的興趣。
二、教學重點:圓的面積計算公式的推導和應用。
教學難點:圓的面積計算公式的推導過程。
三、教學過程:
(一)創設情境,激發興趣。
1.出示情境圖,提出問題:拴在書上的馬兒的最大活動範圍在哪裡?那麼這個最大的活動範圍是什麼呢?如果拴馬兒的繩長是2米,馬兒的最大活動範圍到底是多大呢?(其實就是求半徑是2米的圓的面積)
2.明確圓的面積的概念:圓所佔平面的大小叫做圓的面積。
(二)探究方法。
1.回想一下,我們是怎樣的到平行四邊形、三角形和梯形的面積公式的?(以平行四邊形為例)。
2.我們將圓轉化成什麼樣的圖形來推導它的面積計算公式呢?
【通過回顧原有的知識體系,激發學生知識的遷移,為後面自主探究圓的面積計算公式奠定了基礎。】
(三)實踐操作。
1.動手試一試,剪一剪並拼一拼,想想怎樣剪拼更好,看看能拼成什麼圖形?並且等分的份數越多會怎樣?
【在剛才這個動手操作的過程中,放手讓學生通過比較得出沿半徑剪拼的方法是較為科學的,在教學中注重對學生進行思維方法的指導,給學生提供了自行探究,創造性尋找解決問題的方法和途徑,再通過電腦課件的演示,生動形象地展示了化曲為直的剪拼過程。使學生進一步明確拼成的平行四邊形與圓之間的對應關係,有效地認識和理解圓轉化成平行四邊形的演變過程。】
2.通過觀察比較,看看當圓轉化成近似的平行四邊形後,它們之間有什麼關係?
(1)圓的形狀發生了變化,但面積的大小沒變。
(2)平行四邊形的底就相當於圓周長的一半,平行四邊形的高就相當於圓的半徑,因為平行四邊形的面積=底×高,那麼圓的面積就是圓周長的一半×半徑,用字母表示為s=∏r×r=∏r2,,所以圓的面積公式是s=∏r2。
【在學生的動手操作,推導中建立數學模型。】
(四)鞏固練習。
1.用所學的知識解決馬兒的困惑。
s=∏r2=3.14×2×2=12.56平方米。
【迴應了開頭,使課堂形成了一個完整的體系,也體現了知識的學有所用。】
2.求下面圓的面積。
(1)r=3釐米 (2)r=1.2米 (3)r=3.5分米
3.已知圓的直徑求圓的面積。出示題目:一個雷達螢幕的直徑是40釐米,它的面積是多少平方釐米? (先求出半徑)
4.已知圓的周長求圓的面積。出示題目:街心花園中圓形花壇的周長是18.84米。花壇的面積是多少平方米? (先求出半徑)
5.總結:知道圓的半徑、直徑或是周長都可以求出圓的面積。
6.易錯點練習(判斷正誤)
(1)直徑是2釐米的圓,它的周長和麵積相等。( )
(2)兩個圓的周長相等,面積也一定相等。 ( )
(3)圓的半徑越大,圓所佔的面積也越大。 ( )
(4)圓的半徑擴大3倍,它的面積擴大6倍。 ( )
(5)半圓的面積是它的整個圓面積的一半。
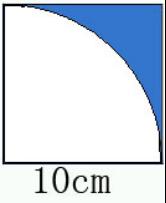
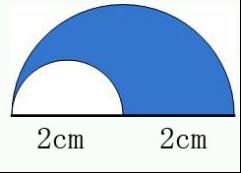
(五)拓展練習:求陰影部分的面積。
【練習由易到難,由淺到深,練習有層次有梯度,課堂容量大,有基礎練習也有易錯點的指導,還有拓展練習,學生的思維得到了提升。】
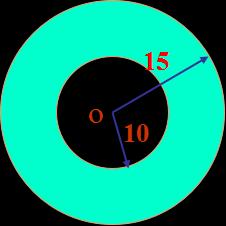
(六)作業。求圓環的面積(連結下節課內容)。