本例子介紹二次函式y=ax^2+bx+c與直線方程y=kx+t,所圍成面積的計算,並介紹拋物線、直線所圍成的區域中,是直線在上,還是拋物線在上,不同情況下的面積計算方法。
工具/原料
二次函式一次函式的基本知識
定積分與面積的關係
冪函式定積分的求法
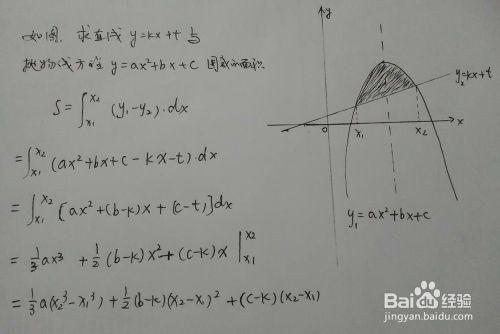
1:圍成面積積分的通用公式
介紹直線y=kx+t,與拋物線y=ax^2+bx+c,並且當拋物線在直線上方時的面積表示式。
2.直線在拋物線下方情形一
本例子主要是在y軸的右方圍成的區域,直線在下方,且二次函式的開口向下。
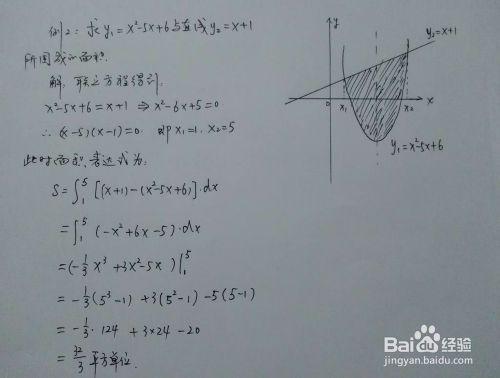
3.直線在拋物線上方的情形一
本例子主要是y軸右方圍成的區域,直線在上方,且二次函式的開口向上。
4.直線在拋物線上方的情形二
本例子主要是y軸左方圍成的區域,直線在下方,且二次函式的開口向下。
5.直線在拋物線下方的情形二
本例子主要是y軸左方圍成的區域,直線在下方,且二次函式的開口向下。
注意事項
面積積分中,積分下限小,上限大。