有件事似乎無所不在:你把手伸到包包裡拿出你的耳機,但是無論之前你把耳機纏得如何整齊,耳機線總是會結成一個十分混亂的結。我們可能會繼續忍受這個問題。
工具/原料
耳機
方法/步驟
近年來,物理學家和數學家一直在反覆研究有線耳機的纏繞問題。通過實驗,科學家們發現有許多途徑能夠解釋繩結科學。2007年,美國加利福尼亞大學的研究員在盒子裡放置了許多線繩並搖晃盒子,以觀察研究為什麼耳機線在你的包裡隨便纏繞亂作一團的原因。他們的論文,“上下襬動的線繩能自然地打結”也解釋了為什麼隨意的搖動總能讓線繩打結,而不是有其他動作。
數學家將繩結分為了不同的種類。比如說,當一條線繩自己纏繞三次後,只能形成一種繩結,被稱為三葉結。同樣,纏繞四次也只能形成一種繩結,叫做八字結。數學家證明出了被稱為“瓊斯多項式”的一系列公式用以定義每一種繩結。結理論在數學領域曾一直是某種充滿奧祕的分支學科
2007年,物理學家Douglas Smith和他當時的本科同學Dorian Raymer決定將扭結理論應用到真實的線繩中去。在一次使用中,他們在盒子裡放置一條線繩並搖晃10分鐘。Raymer以不同長度和不同軟硬度的的繩子、不同尺寸的盒子、以及不同的搖晃頻率重複了三千次。
他們發現,一根線繩在快速搖晃後打結的概率會達到50%。而且,這也與線繩的長度有很大的關係。比較短的繩子——少於一個半英尺——一般不會打結。越長的線繩,打結的可能性就越大。但是這一概率隨繩結變長到一定程度就停止了。超過5英尺的繩子在盒子裡就會無計可施。
Raymer和Smith也利用數學家推算出的瓊斯多項式給所形成的繩結分了類,每次搖晃之後,他們都會給線繩拍一張照片並將照片上傳至一個用於給繩結分類的電腦算法程序中。扭結理論對於少於等於7個結的初級繩結給予14種分類。然而二人還發現了更加複雜的繩結,有些繩結竟然高達11個結。
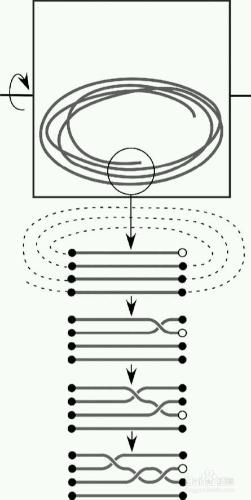
研究員們創造了一個模型用以解釋他們的觀測結果。為了適應盒子,線繩必須要以一種捲曲的姿態待在其中,這意味著繩子末端與繩子的不同部分會平行排放。隨著盒子晃動,繩子末端有充分的機會上下翻滾並與繩子中段的諸多部分相遇。如果搖晃了充足時間,繩子末端就會與繩子中部纏繞在一起,從而形成不同的繩結。
這些實驗所要解決的最重要的問題就是,如何讓繩子保持不纏繞不打結。一種能夠降低繩子打結機率的方法就是在繞線盒裡放置一些比較硬的繩子。
更小的容器體積也是防止打結的妙招之一。小盒子將較長的線繩緊緊束縛住,從而阻止了線繩上下移動並打結。