小學三年級列表解決問題—巧解“繩子與井”問題?

《繩子量井深》明代珠算家程大位在其鎖住的《直指算法統宗》中有記載，通常小學數學教學中採用的是——等量代換方法和比較法，但是都不是很直觀，這裡採用繪圖法和等量替換法結合方便小學生理解。

工具/原料

用一根繩子測量一口井的深度，把繩子折成相等的三段後去測量，井口外餘下3米。如果把繩子折成相等的四段後去測量，井口外餘下1米。這口井深（）米，繩子長（）米。

方法/步驟

對於小學生來講，這道題的關鍵是理解在兩次折繩的過程中，繩子的長度和井的深度是不變的。

繪圖分析：

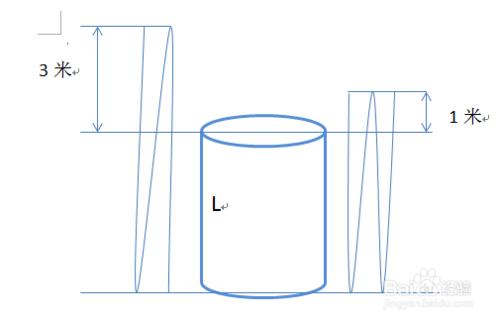
如圖，左側的繩子折3次，得到的效果，繩子的長度=井外繩子的長度+井內繩子長度=井外的繩長（3×3=9米）+井內的繩長（3倍井深）。

如圖，右側的繩子折4次，得到的效果，繩子的長度=井外繩子的長度+井內繩子長度=井外的繩長（4×1=4米）+井內的繩長（4倍井深）。

利用數學思維——等量替換法

因為繩長是固定長度，所以

井外的繩長（3×3=9米）+井內的繩長（3倍井深）=井外的繩長（4×1=4米）+井內的繩長（4倍井深）

因此，井深=9米-4米=5米

繩長=井外的繩長（3×3=9米）+井內的繩長（3倍井深）=9米+（5*3）米=24米

或

繩長=井外的繩長（4×1=4米）+井內的繩長（4倍井深）=4米+（5*4）米=24米