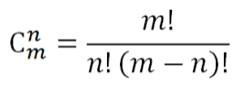排列組合、計數原理在高考數學理科中一般是一道選擇或者填空題,分數不大,但是如果做的方法不對,可能消耗時間過多。
1.計數原理包括分類計數原理和分步計數原理。
分類計數,表示完成一件事有n類方法,每一類完美完成,第i類有mi種方法。
N=m1+m2+...+mi
分步計數,表示完成一件事必須經過n個步驟,每一步都是完成這件事的必經步驟,
第i步有mi種方法
N=m1*m2*...mi
2. 排列和排列數
方法/步驟
3. 組合和組合數
從m個不同元素中,任取n(n≤m)個元素併成一組,叫做從m個不同元素中取出n個元素的一個組合;從m個不同元素中取出n(n≤m)個元素的所有組合的個數,叫做從m個不同元素中取出n個元素的組合數。
例1
由3枚一分硬幣,6枚一角硬幣和4張10元紙幣,共可組成多少種非零幣值?
分析題目,此題屬於分類,分步計數原理
例2
7人排隊拍照
(1)甲不在中間,乙在右邊的排法有多少種?(2)甲與乙、丙二人都不相鄰的排法有多少種?
此題屬於排列問題。
第一問,乙在右邊,實際上可以只考慮其餘6人的位置排列。甲不在中間,即只能在6個剩餘的位置中挑1個位置。然後其他人全排列。
第二問,要先考慮安排甲的位置。