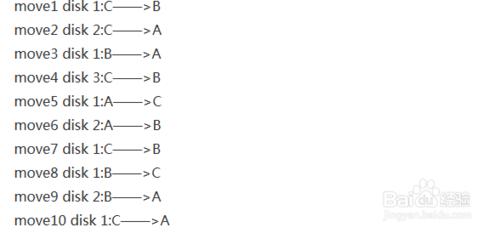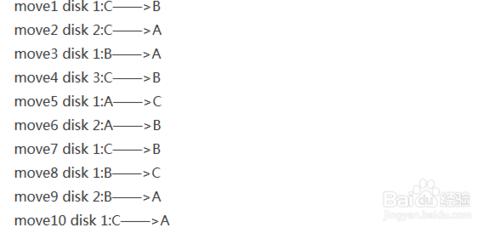遞歸的應用,這是新漢諾塔,在這個程序以及算法的設計實現中我學習到了很多的邏輯處理的能力,算法很有意思,值得好好的推敲學習。
工具/原料
eclipse-luna
jdk1.7
方法/步驟
應用新漢諾塔遊戲
假設有不同大小的光碟標籤ñ從1到n按照它們的大小的升序排列。在初始狀態是隨機的N光盤上三極堆積,現在你必須要了解最少的動作把初始狀態的目標。該舉措的要求為以下幾種: 1)你只能一次移動一個圓盤;2)較大的光盤是不允許在一個較小的一棧
current和target分別表示開始狀態的結束狀態。
算法設計思路
基本的漢諾塔移動算法:
漢諾塔的分析:
第一,把a上的n-1個盤通過c移動到b。
第二,把a上的最下面的盤移到c。
第三,因為n-1個盤全在b上了,所以把b當做a重複以上步驟就好了。
形成一摞的k-1盤子的算法:
make_tower(k,current)
if k=1 then return
if k=2
if current[k]≠current[k-1]
then 將k移到k+1上
return
if k,k-1,k-2分別位於不同位置
then make_tower(k-2,current)
將k-1移到k上
Hanoi(current,k-2,current[k-2],current[k-1],current[k])
return
make_tower(k-1,current)
if k和k-1不在同一個位置
then temp←除k和k-1的位置
Hanoi(current,k-1,current[k-1],temp,current[k])
全部程序實現:
package ch2.divide;
public class NewHanoi {
public static int count = 0;
// /這個地方的用途就是找到A杆頂端要移動的盤子的編號i
// //將 這個盤子移動到C杆上,修改current[i]的值為C
// //累加移動盤子的次數然後輸出A——>C的信息
// //找出當前需要移動的杆子(根據ABC符號進行識別)的頂部盤子的編號i
// //修改當前編號的盤子所在的杆子的符號
// ---這個函數的作用是尋找發現當前移動的盤子所在杆子的狀態變化的一個記錄修改-----//
private static int pickTopDisk(char[] current, char a) {
int i = 1;
while (current[i] != a) {
i++;
}
return i;
}
// 漢諾塔基本的搬運算法
public static void hanoi(char[] current, int n, char A, char B, char C) {
if (n == 1) {
int i;
i = 1;
i = pickTopDisk(current, A);
current[i] = C;
count++;
// /只有一塊圓盤 , 直接移至c
System.out.println("move" + count + " disk " + i + ":" + A + "——>" + C);
return;
}
// /第一,把a上的n-1個盤通過c移動到b
hanoi(current, n - 1, A, C, B);
current[n] = C;
// 這裡第n個盤子就是下標為n-1,一定要記在心裡
count++;
System.out.println("move" + count + " disk " + n + ":" + A + "——>" + C);
hanoi(current, n - 1, B, A, C);
}
////將小於目標盤的所有盤摞成一個塔的形狀(小盤位於大盤之上)
public static void makeTower(char[] c, int n) {
char temp; //臨時的字符聲明
//------n=1和n=2特殊情況可以直接處理--------///
if (n == 1)
return;
///將1號盤子移動到2號盤子之上
if (n == 2) {
if (c[1] != c[2]) {
count++;
System.out.println("move" + count + " disk " + 1 + ":" + c[1] + "——>" + c[2]);
c[1] = c[2];
}
return;
}
//情況1------n=1和n=2特殊情況可以直接處理--------///
//情況2------n,n-1,n-2都不在同一個盤子上--------///
if (c[n] != c[n - 1] && c[n] != c[n - 2] && c[n - 1] != c[n - 2]) {
makeTower(c, n - 2);
// 將n-1移到n上
count++;
System.out.println("move" + count + " disk " + (n - 1) + ":" + c[n - 1] + "——>" + c[n]);
temp = c[n - 1];
c[n - 1] = c[n];
hanoi(c, n - 2, c[n - 2], temp, c[n-1]);
return;
}
//情況2------n,n-1,n-2都不在同一個盤子上--------///
makeTower(c, n - 1); //這個地方自由的遞歸實現不斷的細化減少盤子的編號
///這個地方是一般情況下,我們會找到一個空餘的位置利用hanoi的基本搬運算法把所有的n-1個盤子移動過去
if (c[n - 1] != c[n]) {
temp = (char) ('A' + 'B' + 'C' - c[n] - c[n - 1]);
hanoi(c, n - 1, c[n - 1], temp, c[n]);
}
}
public static void main(String[] args) {
///字符數組中的0用來佔據位置作為數組中國0這個位置的站位字符 在實際的操作中不使用
char[] current = { 0, 'C', 'C', 'C', 'B', 'B' };
char[] target = { 0, 'C', 'A', 'C', 'B', 'C' };
int k = 5;
char temp;
//找到第一個最大的不符合要求的盤子
while (current[k] == target[k] && k > 0)
k--;
// 如果k>2,把1...k-1移到k-1上 形成一摞有序的k-1盤子
if (k > 2)
makeTower(current, k - 1);
while (k > 1) {
///騰出目標位置
if (current[k] != target[k]) {
if (current[k] == current[k - 1]) {
////如果k-1個盤子在current[k]上面,將其移動到空閒的杆子上面
temp = (char) ('A' + 'B' + 'C' - current[k] - target[k]);
hanoi(current, k - 1, current[k - 1], target[k], temp);
} else if (current[k - 1] == target[k]) {
////如果k-1個盤子在target[k]上面,將其移動到空閒的杆子上面
temp = (char) ('A' + 'B' + 'C' - current[k] - target[k]);
hanoi(current, k - 1, current[k - 1], current[k],temp);
}
count++;
///將第k個盤子移動到目標位置
System.out.println("move" + count + " disk " + k + ":" + current[k] + "——>" + target[k]);
current[k] = target[k];
}
k--;
}
if (current[1] != target[1]) {
count++;
System.out.println("move" + NewHanoi.count + " disk " + 1 + ":" + current[1] + "——>" + target[1]);
current[1] = target[1];
}
}
}
運行結果:
move1 disk 1:C——>B
move2 disk 2:C——>A
move3 disk 1:B——>A
move4 disk 3:C——>B
move5 disk 1:A——>C
move6 disk 2:A——>B
move7 disk 1:C——>B
move8 disk 1:B——>C
move9 disk 2:B——>A
move10 disk 1:C——>A
move11 disk 3:B——>C
move12 disk 1:A——>B
move13 disk 2:A——>C
move14 disk 1:B——>C
move15 disk 4:B——>A
move16 disk 1:C——>A
move17 disk 2:C——>B
move18 disk 1:A——>B
move19 disk 3:C——>A
move20 disk 1:B——>C
move21 disk 2:B——>A
move22 disk 1:C——>A
move23 disk 5:B——>C
move24 disk 1:A——>C
move25 disk 2:A——>B
move26 disk 1:C——>B
move27 disk 3:A——>C
move28 disk 1:B——>A
move29 disk 2:B——>C
move30 disk 1:A——>C
move31 disk 4:A——>B
move32 disk 1:C——>B
move33 disk 2:C——>A
move34 disk 1:B——>C
注意事項
maketower是程序設計的重點
注意在主程序中獲取空閒位置放置current[k-1]
只要是完成前兩部分基本就可以根據target實現放置