我們知道任何數據都是以有限位數的二進制來表示,那麼IEEE標準的浮點數也不列外,其中雙精度浮點數是用64位二進制表示,單精度浮點數用32位二進制表示。因此,不能以任意精度表示每一個實數。對於計算機中的浮點數,數與數之間存在最小間隔,這個間隔隨著數的增大而不斷增大,因此也叫相對精度(matlab幫助文檔中稱為Floating-point relative accuracy)。也就是一個數與計算機中能表示的與該數最近的一個數之間的間隔。可進一步參見:http://blog.sina.com.cn/s/blog_4513dde60100o6rl.html和
工具/原料
matlab
方法/步驟
在matlab中通過eps函數來求解某數的浮點相對精度,下面給出示例代碼
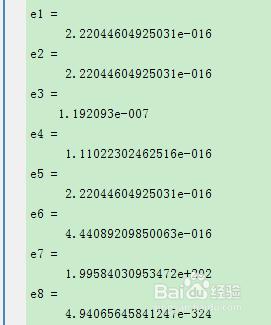
e1=eps
e2=eps('double')
e3=eps('single')
e4=eps(1/2)
e5=eps(1)
e6=eps(2)
e7=eps(realmax)
e8=eps(0)
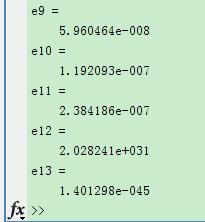
e9=eps(single(1/2))
e10=eps(single(1))
e11=eps(single(2))
e12=eps(realmax('single'))
e13=eps(single(0))
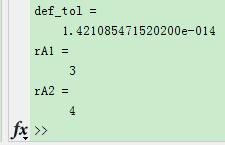
eps函數的一個用法是在需要考慮數字計算精度對結果的影響時,比如matlab中自帶的求矩陣的秩的rank函數默認返回的是奇異值大於max(size(A))*eps(norm(A))的個數,比如下面代碼執行的結果為
U=[
-0.379274725817546 0.794481008161344 0.040314689302254 0.472573101068419
-0.548121117865938 -0.158656907114637 0.785308487819421 -0.240170366475522
-0.701132103179362 -0.096930884878865 -0.615158038749589 -0.347273328675907
-0.253234469211253 -0.578128287711604 -0.056972731609046 0.773559367084354];
V=[-0.395899761267122 0.174787331274778 -0.893374215953781 -0.120810918891644
-0.579336710586230 -0.801660599750723 0.083470911224132 0.121416084411623
-0.442564352640226 0.452790460112304 0.183006779832243 0.752081186800241
-0.558362918331707 0.348956259242386 0.401775603768836 -0.636424971841809];
A=U*diag([10 20 30 1e-15])*V';
def_tol=max(size(A))*eps(norm(A))
rA1=rank(A)
rA2=rank(A,1e-16)