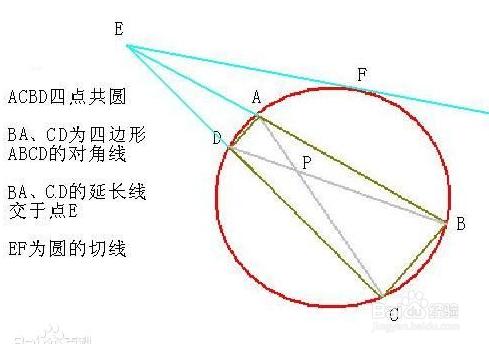
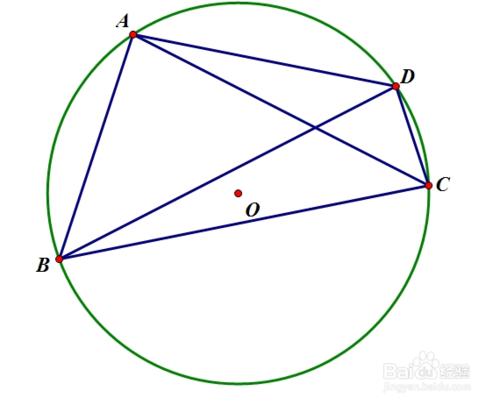
如果同一平面內的四個點在同一個圓上，則稱這四個點共圓，一般簡稱為“四點共圓”。
”三點共圓“是初高中數學幾何證明中的難點，許多同學叫苦不迭。
下面，我就來介紹幾種可以方便證明的思路，供大家參考使用。
工具/原料
圓規、直尺、三角板
聰明的幾何頭腦
草稿紙
方法/步驟
證明方法其實非常簡單。
下列五種基本方法中的每一種的根據，就是產生四點共圓的一種原因。
因此當要求證四點共圓的問題時，首先就要根據命題的條件，並結合圖形的特點，在這五種基本方法中選擇一種證法，給予證明即可。
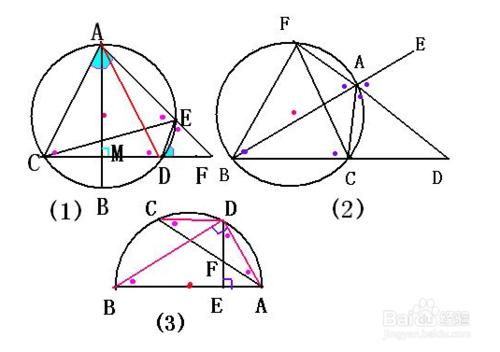
從被證共圓的四點中先選出三點作一圓，然後證另一點也在這個圓周上，若能證明這一點，即可肯定這四點共圓．
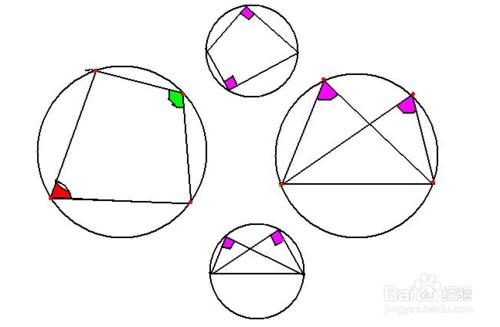
同側，若能證明其頂角相等(同弧所對的圓周角相等），從而即可肯定這四點共圓． （若能證明其兩頂角為直角，即可肯定這四個點共圓，且斜邊上兩點連線為該圓直徑。）
把被證共圓的四點連成四邊形，若能證明其對角互補或能證明其一個外角等於其鄰補角的內對角時，即可肯定這四點共圓．
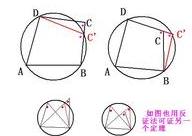
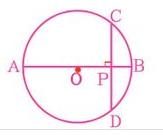
把被證共圓的四點兩兩連成相交的兩條線段，若能證明它們各自被交點分成的兩線段之積相等，即可肯定這四點共圓（相交弦定理的逆定理）；或把被證共圓的四點兩兩連結並延長相交的兩線段，若能證明自交點至一線段兩個端點所成的兩線段之積等於自交點至另一線段兩端點所成的兩線段之積，即可肯定這四點也共圓．（割線定理的逆定理）
證被證共圓的點到某一定點的距離都相等，從而確定它們共圓．即連成的四邊形三邊中垂線有交點，可肯定這四點共圓．
數學, 幾何, 共圓, 中考數學幾何證明題, 初一數學幾何證明題, 初中數學幾何證明題, 七年級數學幾何證明題, 八年級數學幾何證明題, 高中數學幾何證明題, 七下數學幾何證明題, 高中數學幾何證明選講, 初二數學幾何證明題,