一些簡單方程的解我們可以很快地手算出來,但是還有很多方程的解我們手算很難算出或者根本無法算出。
比如解一道一元高次非線性方程,我們一般的解法是先確定方程的解所在的大致範圍,然後用牛頓迭代法來算,很複雜。
這裡我介紹用matlab來解方程,一個命令即可輕鬆得出方程的所有解。
工具/原料
Matlab
解一元方程
先舉一例,解方程"x^2+100*x+99=0"
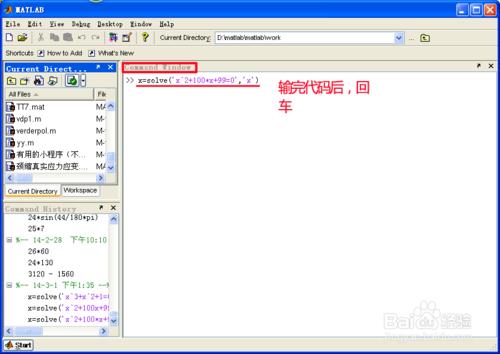
在matlab ”Command Window"中輸入如下命令:
x=solve('x^2+100*x+99=0','x')
見下圖
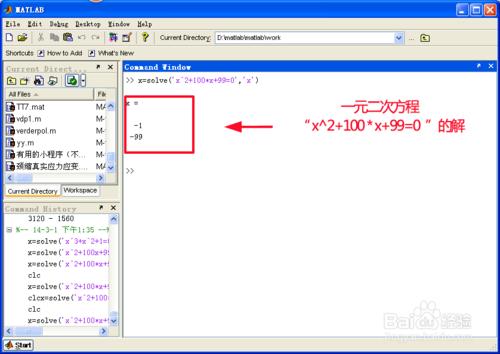
回車後,matlab就求出了這個一元二次方程的解。
見下圖
再舉一例
解一元三次方程"x^3+1=0"
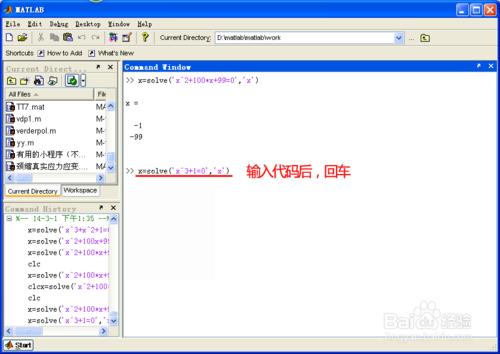
在matlab ”Command Window"中輸入如下命令:
x=solve('x^3+1=0','x')
見下圖
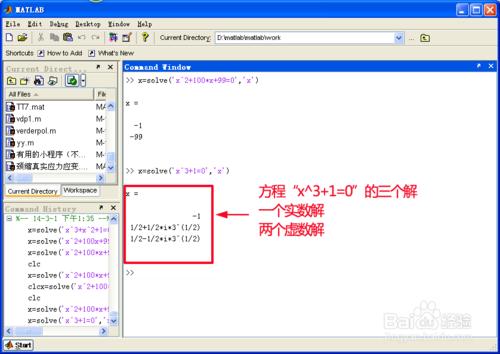
回車後,matlab就求出了這個一元三次方程"x^3+1=0"的解。
見下圖.
matlab解出來的解有三個,其中有一個實數解,兩個虛數解。
我們都知道一元三次方程在複數範圍內的解有3個,matlab的解是對的。
如果我們只要"x^3+1=0”的實數解,我們只要取下面圖中的第一個解“-1”。
解二元方程
首先來求一個二元一次方程組
9x+8y=10 式1
13x+14y=12 式2
我們一般的解法是代入法,或者加減消去法。比較繁瑣。
這裡我們只需輸入如下命令即可求出解:
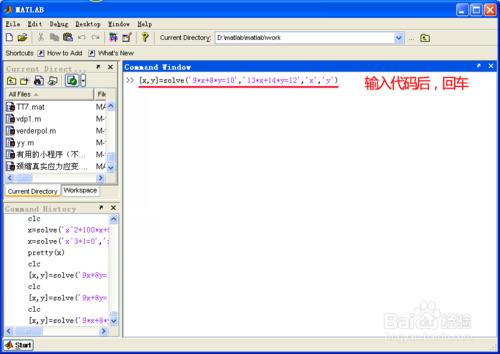
[x,y]=solve('9*x+8*y=10','13*x+14*y=12','x','y')
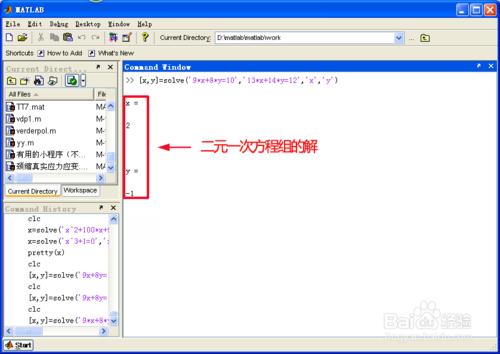
回車後,matlab就求出了這個二元一次方程組的解。
見下圖
再來求一個二元非線性方程組
x^2+y^2=10 式1
2x+3y=0 式2
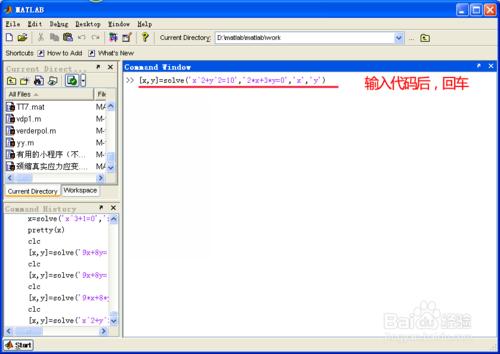
這裡我們只需輸入如下命令即可求出解:
[x,y]=solve('x^2+y^2=10','2*x+3*y=0','x','y')
x^2+y^2=10 式1
2x+3y=0 式2
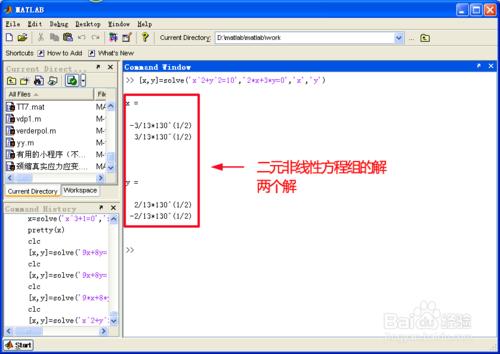
其實不少人能看出來,上面的二元非線性方程組的解是一個圓與一條直線的交點座標,我們的一般解法是先消去y,整理成關於x的一元二次方程,然後求出x值,再求出對應y值。
但這裡,我們只用到了上面圖片裡的的一句命令,就求了這兩個交點座標。見下圖。
解其他方程
解三元方程或更高方程的具體操作步驟我就不再說明了,大家可以參考前面所說的解一元方程到解二元方程的命令的變化,從而類比出來。
相信聰明的讀者讀到這裡,也發現matlab的這個解方程的功能十分簡單實用吧。
前面舉的例子都是比較簡單的,其實matlab一般能解出所有存在解的方程的。
大家加油!