我們知道,正則表達式可以巧妙用來判斷一個整數是否是素數,那麼更進一步,我們來看如何通過正則表達式,求解代數方程中一類著名的問題,丟番圖方程,即整數範圍內的整係數方程。
工具/原料
Chrome
方法/步驟
我們同樣在Chrome瀏覽器中,來執行相應的JS代碼,
來實現使用正則表達式,來求解一些簡單的丟番圖方程,
例如,
小學奧數題中經常出現的雞兔同籠問題。
1500年前,《孫子算經》中就記載了這個有趣的問題:
今有雉兔同籠,上有三十五頭,下有九十四足,問雉兔各幾何?
雉【zhì】,俗稱“野雞”。這句話意思就是
把雞和兔放在同一個籠子中,數頭有35個頭,數腳有94只腳,
那麼雞和兔分別有多少隻?
我們知道,設雞和兔分別為x和y只,可以這樣列二元一次方程組:
x+y=35
2x+4y=94
並求它的正整數解。
在正式解方程之前,我們先來看如何使用正則表達式
來解多元一次方程的正整數解。
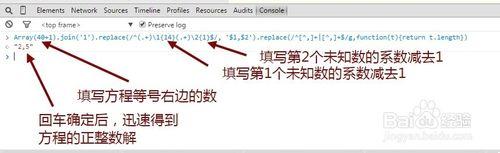
舉例這個二元一次方程:15x+2y=40
首先,我們在Chrome瀏覽器中,打開Console控制檯
方法是,在任何網頁,按下快捷鍵F12(或者右擊“審查元素”)
然後點擊“Console”
我們正式輸入JS代碼(其中用到了正則表達式)
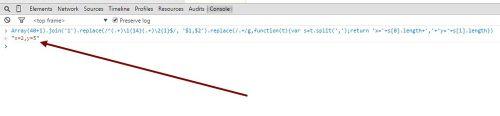
Array(40+1).join(1).replace(/^(.+)\1{14}(.+)\2{1}$/, '$1,$2').replace(/^[^,]+ [^,]+$/g,function(t){return t.length})
然後按下回車鍵,迅速得到方程的正整數解
注意,上述代碼中加粗部分,分別為:
40:即方程等號右邊的數字
14:第一個未知數的係數減去1
1:第二個未知數的係數減去1
可以驗算一下,(2,5)確實是方程15x+2y=40的一組正整數解。
這裡來詳細解釋一下,上面JS代碼的原理。
Array(40+1) // 構建一個包含(40+1)個元素的空數組
.join(1) // 將數組中元素用字符串1連接起來,
// 變成一個40個1組成的字符串
.replace(/^(.+)\1{14}(.+)\2{1}$/, '$1,$2') // 將40個1的字符串,
// 進行正則表達式匹配,
// 匹配為(14+1)個子字符串,
// 以及(1+1)個子字符串
// 這兩個子字符串合起來,即組成原來的40個1的字符串
// 匹配成功後,在這兩個子字符串之間,插入英文半角逗號
.replace(/^[^,]+ [^,]+$/g,function(t){return t.length})
// 根據逗號分隔標記,分別計算這兩個子字符串的長度,
// 用長度來代替原來的字符串,即可得到方程的解
當然最後的替換,我們還可以這樣來寫,
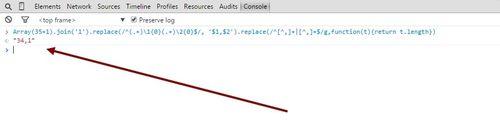
.replace(/.+/g,function(t){var s=t.split(',');return 'x='+s[0].length+','+'y='+s[1].length})
// 得到x=2,y=5更加直觀的求解結果。
接下來,我們正式回到一開始的雞兔同籠問題。
注意,如果直接按照上述思路,來求解,很可能失敗。
舉例,方程組中的第1個方程,x+y=35
因為有很多組解,如果簡單使用上述代碼,會得到這樣的錯誤解
那麼如何解決這個困難,尤其在有多個方程(二維甚至更多維)的情況下呢?
我們可以嘗試使用for循環,來遍歷未知數所在的正整數範圍,進行求解。
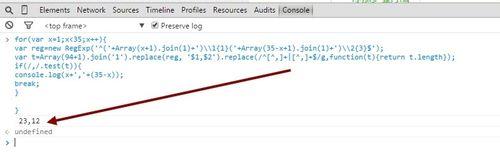
for(var x=1;x<35;x++){
var reg=new RegExp('^('+Array(x+1).join(1)+')\\1{1}('+Array(35-x+1).join(1)+')\\2{3}$');
var t=Array(94+1).join(1).replace(reg, '$1,$2').replace(/^[^,]+ [^,]+$/g,function(t){return t.length});
if(/,/.test(t)){
console.log(x+','+(35-x));
break;
}
}
即可得到正確解;
23,12
注意事項
儘量先計算一下變量精確的約束範圍,提高正則表達式求解方程的有效性
如果方程係數不為整數,可以先轉化成整係數方程
使用正則表達式求解方程,效率很低,僅作興趣參考研究