多元方差分析就是有多個因變數的分析,但是這幾個因變數並不是沒有關係的,他們應該屬於同一種質的不同的形式,比如一個問卷的幾個不同的維度。下面我們來具體的操作一下多元方差分析。
方法/步驟
在spss中開啟資料,在選單欄上執行:analyse--general linear model--multivariate,開啟多元方差分析對話方塊
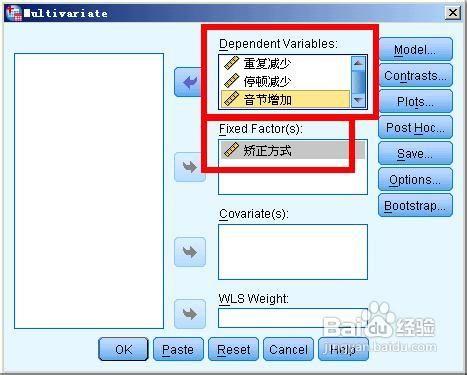
將所有的因變數都放到第一個列表裡,將自變數放到固定因素列表裡
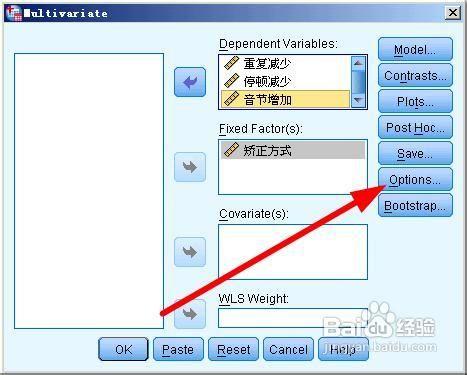
點選options按鈕,開啟子對話方塊
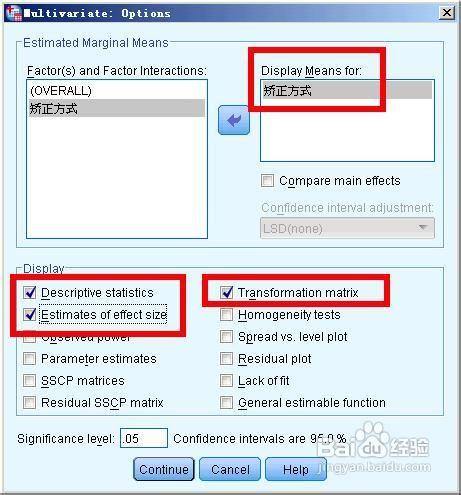
將自變數矯正方式放到右側的display means,勾選如圖所示的三個選項,用來展示描述統計、方差齊性、效應大小,點選繼續,返回到主對話方塊
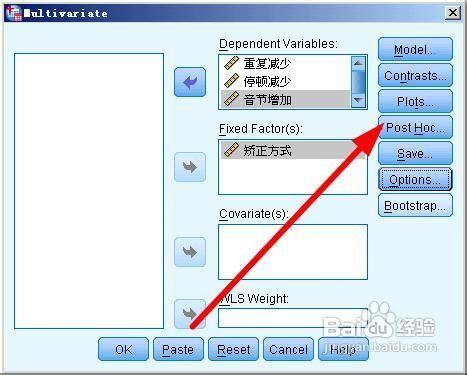
點選post hoc,設定事後檢驗
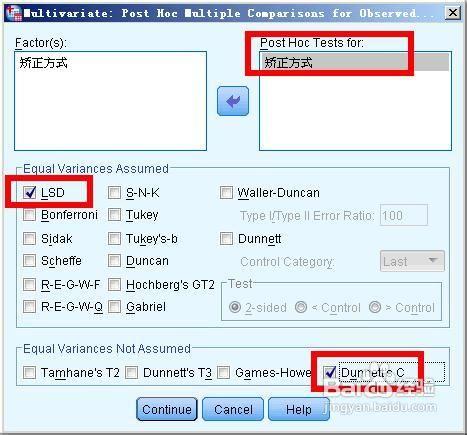
將自變數矯正方式放到事後檢驗的列表裡,然後在方差齊性的方法中選擇lsd,在方差不齊性的方法中選dunnet c,點選continue按鈕
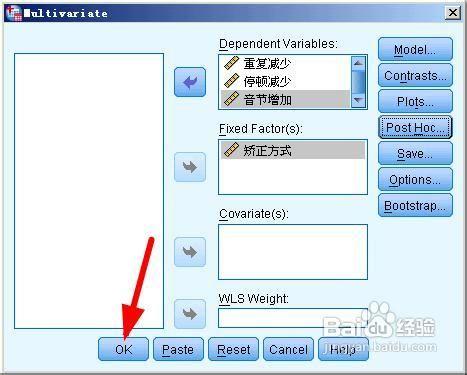
點選ok按鈕,開始資料處理
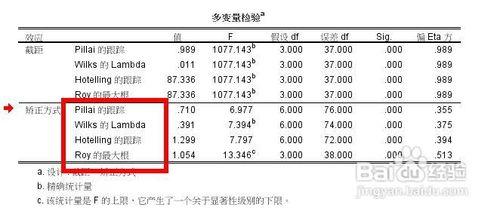
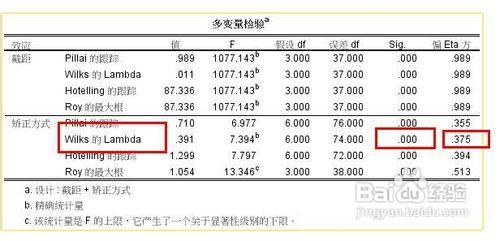
我們先來分析多變數檢驗,如圖所示的紅色方框中顯示的是檢驗的不同方法,有時候不同的方法會顯示出不同的結果,你要分別解釋,下面的結果是一致的
我們以wilks lambda方法為例,看sig值為000說明差異顯著,篇eta方位0.375說明可以解釋變異的37.5%
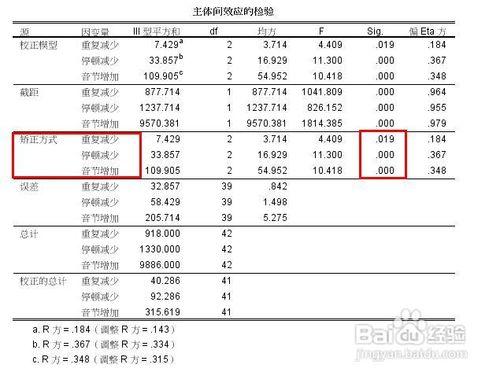
接著看主體間效應的檢驗,在矯正方式這一欄,也就是自變數的這一欄,乍一看三個水平的自變數都達到了顯著水平,但是,其實不然,因為對自變數的多次比較會造成一類錯誤的概率增加,所以我們要用顯著性水平除以自變數的水平數,也就是0.05/3=0.17,這樣來看重複減少這個水平是達不到顯著水平的。