在高中接觸到圓錐曲線的各位肯定和我一樣深惡痛絕圓錐曲線。繁瑣的計算,千篇一律的解題方法,看不懂的解析,以及一些有那幕大的引數,這些都是影響高中生考場拿分和考後總結,平時練習的因素,不過現在我會來教你應該如何巧妙地解決圓錐曲線,成就大神!
工具/原料
一顆對數學飽含深情的心,一支筆,一張紙
方法/步驟
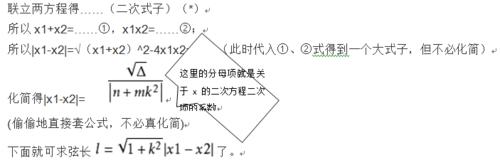
一.直線方程與橢圓方程的聯立——設y=kx+b,再用韋達定理
Ps. 1)為了防止把b看成6,一般設y=kx+m 2)定點(0,m)在y軸上,設直線為y=kx+m。定點(n,0)在x軸上,設直線為x=ky+n。利於聯立方程的求解 3)變換直線方程的形式,對合求解
通常對合解法常與座標軸的平移,斜率的相乘相加有關,但相對於極座標和引數方程略顯複雜
2.圓的諸多性質——仿射基礎
1)切割線定理
2)相交弦定理(多次遇見不做詳細解釋)
3)垂徑定理:垂直於弦的直徑平分弦且平分這條弦所對的兩條弧。
4)扇形面積:(類比三角形的底稱高除以二)弧長乘半徑除以二,S= 0.5LR
5) 阿波羅尼圓Apollonius:平面內到兩個定點的距離之比為常數k(k≠1)的點的軌跡是圓,這個圓就是阿波羅尼圓。
已知:定點M(c,0),N(-c,0),P(x,y)
求證:平面內到兩個定點M,N的距離之比為常數k(k≠1)的點P的軌跡是圓
證明:d1比d2 =k(d用點到點距離公式帶)
通分後化簡得(k²-1)x²+(k²-1)y²+(k²+1)x+(k²-1)c²=0
約分 x²+y²+(k²+1)/(k²-1)x+c²=0
此形式為圓的一般方程。
三.引數方程的用法
引數方程一般聯立時切勿使用,因為一個cos,sin下來,答題紙就不夠寫的了
拋物線一般設直方最簡單,不用引數
引數方程最大的好處就是求範圍比較舒服,而且式子中的轉化比較明顯。
四,點差法——高中最有用的方法
相比起一些不靠譜的神技能,點差法可謂是圓錐曲線官方認可的一個大bug
五.極點極線的用法和性質——站在出題人的角度思考答案
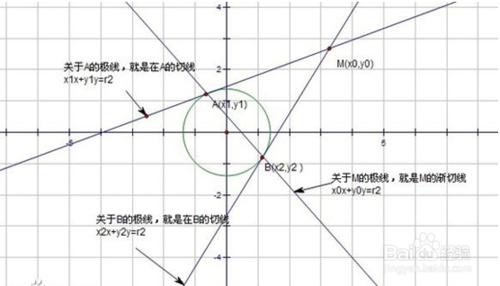
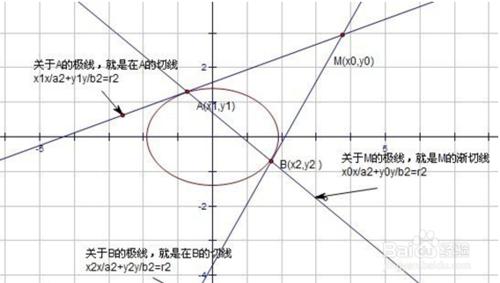
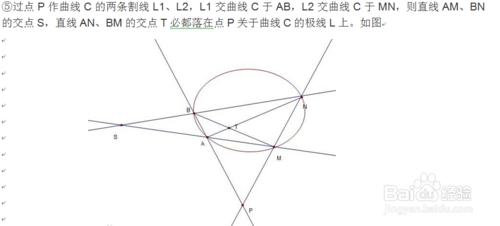
定義: 對於二次曲線C:Ax²+By²+Cx+Dy+E=0和一點P(x0,y0) 其中A²+B²≠0,P不在曲線的中心和漸近線上 用x0*x代x²,yo*y代y²,(x0+x)/2代x,(yo+y)/2代y,得到一條直線方程 則稱點P和直線l是關於曲線C的一對極點和極線 即點P是直線l關於曲線C的極點,直線l是點P關於曲線C的極線。 特殊的,焦點和準線是曲線的一對特殊的極點和極線
其實,圓與橢圓的切線與漸切線就是特殊的極線,如圖
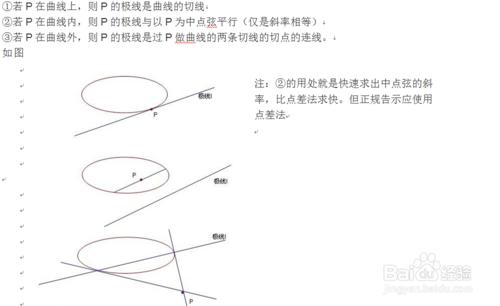
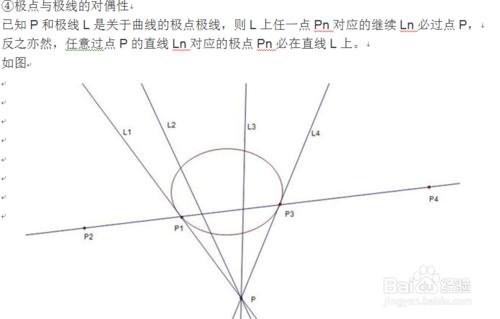
極點極線的性質: 一般的有如下性質(焦點所在區域為曲線內部)
Ps.學完極點極線後兩個毛病 1.知道是極點極線就不想算了 2.啥題型都往極點極線靠
六.仿射在圓錐曲線的妙用
1.橢圓如何化圓?
七,極座標與圓錐曲線的結合
八,特殊公式
九,圓錐曲線的幾何意義
補充:
橢圓內最大矩形面積為2ab(可用仿射法推導)。
雙曲線焦點到漸近線距離為b