本文介紹使用Excel的規劃求解模塊,解決服務設施定位的問題,在運籌學中被稱為覆蓋問題。
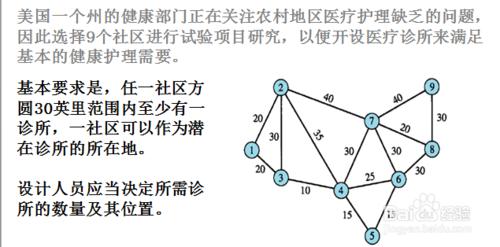
如下圖所示,考慮滿足條件(每個社區30英里範圍內至少有一家診所)的前提下,診所總數越少越好。自變量是診所的位置——對應九個社區的9個二分變量(0表示不設診所,1表示設診所)。
工具/原料
Excel 2010
方法/步驟
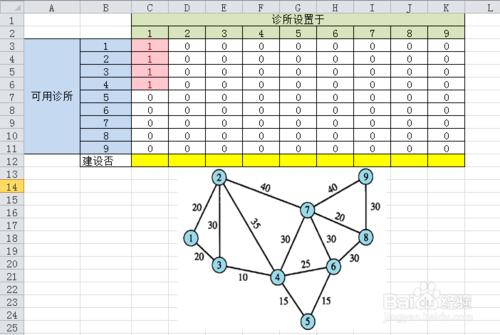
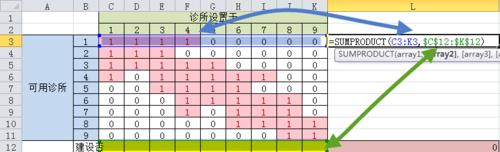
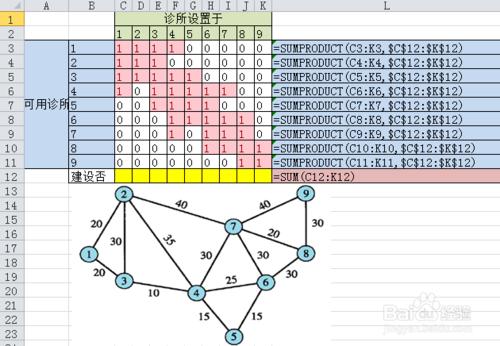
1.設置可達性矩陣
列C到列K表示診所建設的事
第3行到第11行就是9個社區可用診所數量的事;
區域【C12:K12】為可變單元格(決策變量)——取值表示建設不建設診所
於是區域【C3:K11】這個矩陣就是“可達性矩陣”
------------
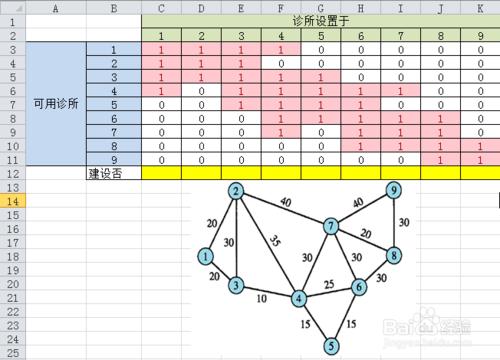
我們以C列為例,如果社區1建設診所(C3=1),那麼根據地圖,我們可以看到
1——>1, 0
1——>2, 20
1——>3, 20
1——>4, 20+10=30
只有這4個社區在30英里範圍內,所以只有【C3】、【C4】、【C5】和【C6】的取值為1(可以抵達,可以覆蓋),【C5】、【C6】、【C7】、【C8】和【C9】取值為0
------------
我們可以先設置可達性矩陣(【C3:K11】)為0,然後1列1列的根據地圖,把可達的邊更改為數值1
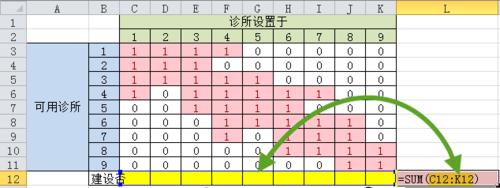
2.目標函數
設置目標函數,在單元格【L12】輸入函數【=SUM(C12:K12)】
3.每個社區可達的診所總數
***在單元格【L3】輸入函數【=SUMPRODUCT(C3:K3,$C$12:$K$12)】
***選中單元格【L3】,移動鼠標,當鼠標呈黑色小十字時,向下拖拽到單元格【L11】
--------------------
sumproduct函數包括兩個單詞,sum(求和)、product(乘法),所以意思“先乘,後求和”
本公式中區域【C4:E5】內的單元格與區域【C11:E12】內的單元格分別先乘後求和,只有可覆蓋(可達性矩陣取值為1)並且建設診所(建設否取值為1)才是現實可達的,求和就是總計的可用診所。
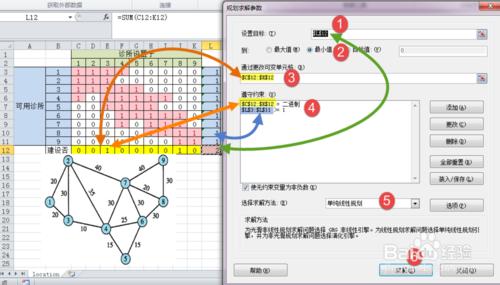
4.規劃求解
點擊【數據】——【規劃求解】
***在彈出的窗口,【設置目標】,點擊右側的按鈕,選中單元格【L12】—— 診所總數
***其下,點選【最小值】—— 最少診所數
***其下,【可變單元格】點擊右側的按鈕,選中區域【C12: K12】——9個自變量
***在【規劃求解】窗口,點擊右側的【添加】,添加2類約束條件
其一、每個社區可用診所數>=1
其二、自變量為二分變量
***求解方法,點選【單純線性規劃
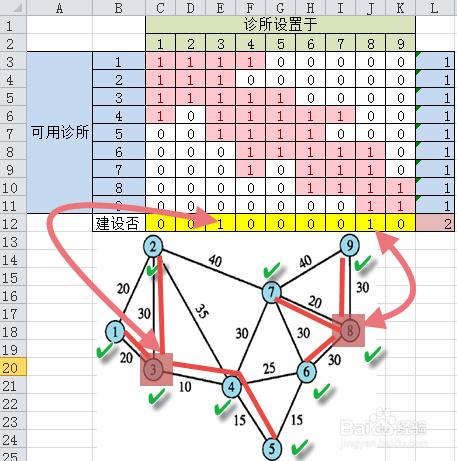
求解結果是,最少建設2個診所可以,分別位於社區3和社區8
-------------
最優解(2個診所)是確定的
建設方案可以有不同,獲取不同方案的方法就是改變初值。