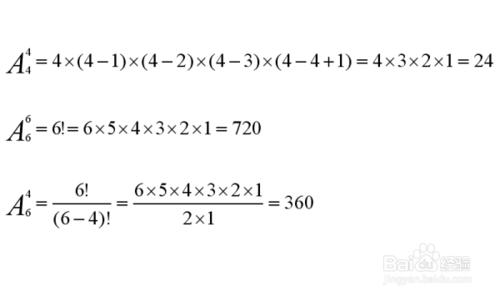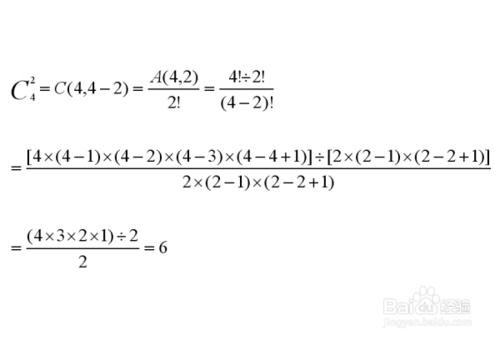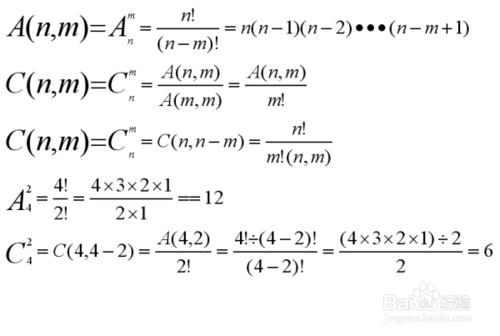看了對排列組合的介紹,只有定義與公式,完全是程序化的說明,發現自己理解的很費力。
為了輔助對排列組合定義的理解,小編用具體的例子來說明它的定義。並列出了詳細的計算過程。
排列的定義及其計算公式
排列有兩種定義,但計算方法只有一種,凡是符合這兩種定義的都用這種方法計算。
定義的前提條件是m≦n,m與n均為自然數。
① 從n個不同元素中,任取m個元素按照一定的順序排成一列,叫做從n個不同元素中取出m個元素的一個排列。
② 從n個不同元素中,取出m個元素的所有排列的個數,叫做從n個不同元素中取出m個元素的排列數。
③ 用具體的例子來理解上面的定義:4種顏色按不同顏色,進行排列,有多少種排列方法,如果是6種顏色呢。從6種顏色中取出4種進行排列呢。
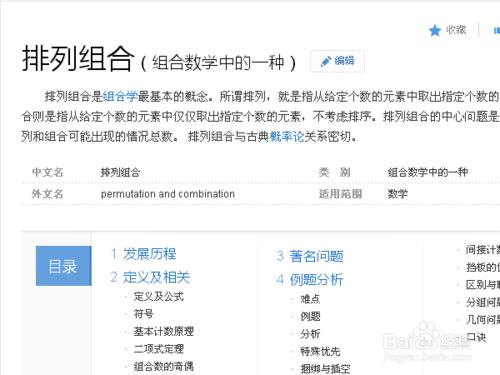
解:A(4,4)=4x(4-1)x(4-2)x(4-3)x(4-4+1)=4x1x2x3x1=24。
A(6,6)=6x5x4x3x2x1=720。
A(6,4)=6!/(6-4)!=(6x5x4x3x2x1)/2=360。
[計算公式]
排列用符號A(n,m)表示,m≦n。
計算公式是:A(n,m)=n(n-1)(n-2)……(n-m+1)=n!/(n-m)!
此外規定0!=1,n!表示n(n-1)(n-2)…1
例如:6!=6x5x4x3x2x1=720,4!=4x3x2x1=24。
組合的定義及其計算公式
組合的定義有兩種。定義的前提條件是m≦n。
① 從n個不同元素中,任取m個元素併成一組,叫做從n個不同元素中取出m個元素的一個組合。
② 從n個不同元素中,取出m個元素的所有組合的個數,叫做從n個不同元素中取出m個元素的組合數。
③ 用例子來理解定義:從4種顏色中,取出2種顏色,能形成多少種組合。
解:C(4,2)=A(4,2)/2!={[4x(4-1)x(4-2)x(4-3)x(4-4+1)]/[2x(2-1)x(2-2+1)]}/[2x(2-1)x(2-2+1)]=[(4x3x2x1)/2]/2=6。
[計算公式]
組合用符號C(n,m)表示,m≦n。
公式是:C(n,m)=A(n,m)/m! 或 C(n,m)=C(n,n-m)。
例如:C(5,2)=A(5,2)/[2!x(5-2)!]=(1x2x3x4x5)/[2x(1x2x3)]=10。
其它排列與組合公式
其它排列與組合有三種。
① 從n個元素中取出m個元素的循環排列數=A(n,m)/m!=n!/m!(n-m)!。
② n個元素被分成K類,每類的個數分別是n1,n2,…,nk這n個元素的全排列數為n!/(n1!xn2!x…xnk!)。
③ k類元素,每類的個數無限,從中取出m個元素的組合數為C(m+k-1,m)。
符號說明
C-代表-Combination--組合數
A-代表-Arrangement--排列數(在舊教材為P-permutation--排列)
N-代表-元素的總個數
M-代表-參與選擇的元素個數
!-代表-階乘
基本公式整理
只要記住下面公式,就會計算排列組合:(在列式中n為下標,m為上標)
排列
A(n,m)=n(n-1)(n-2)……(n-m+1)=n!/(n-m)!
組合
C(n,m)=A(n,m)/A(m,m)=A(n,m)/m!
C(n,m)=C(n,n-m)=n!/m!(n,m)!
例如
A(4,2)=4!/2!=4x3=12
C(4,2)=4!/(2!x2!)=(4x3x2)/(2x2)=6