橢圓是高中的一大壓軸題,很多同學在這裡都會犯難,如果沒有正確的方法去解決,一味的去作相關的題,而不得到總結,勢必其反,在這就我的做題經驗給予分享。
工具/原料
一顆清醒的大腦
一顆能耐得下來的心
方法/步驟
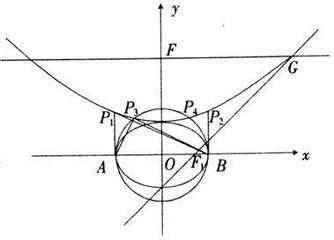
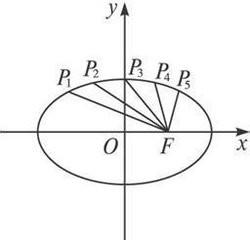
橢圓,起步最基礎的就是要懂得他的基本性質,比如相關參數A,B,C值的幾何含義,基本圖形的樣式,給自己的大腦以橢圓一個最基本的認識。可別小看這些性質,是我們解題必備的不可或缺的基礎!!!
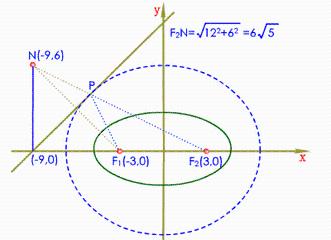
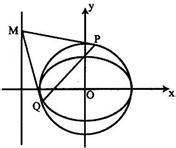
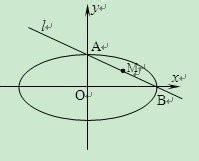
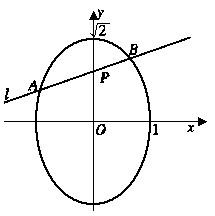
接下來就是我們常見的題型,幾乎考試都會出現的橢圓與直線的問題 了。關鍵的在於直線於橢圓的相交知識,幾乎必考。遇到直線,我們就要先設出直線方程,然後與橢圓方程聯立,因為交點幾乎都要用到這個。此時你會發現,聯立的是一大片又一大片的數字於字母,有時候是很多的很多的字母要整理,不要怕,瞄準X的平方項 與一次項,不要去解X,先放著,一般多設計(X1+X2),常數項不要去理他。如果的如果真的要算出X=?那就首選十字相交法,一般都是可行的。
別小看x1 + x2 =? 大題中我統計過十有八九是要這個式子的,遇到交點就朝著這個方向,然後在根據題目的意思,去找關係,找等式,一般是線段相等,或向量相等,更加高級的一些就是設計面積的問題,不要怕,依據題目的關係就耐心的去列個等式,你會發現,有解了!!
橢圓的主體思想就是要鍛鍊學生 們的方程思想,方程思想是什麼?就不是等式嗎?還有一個最大 的傷痛處就是運算,這是數學修養的必備東西,對於運算,我們也不要怕,還記得初中的多項式整理嗎?那麼複雜的整理我們都 過來了,這點小問題我們一個一個去分開來解決。
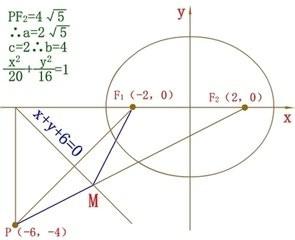
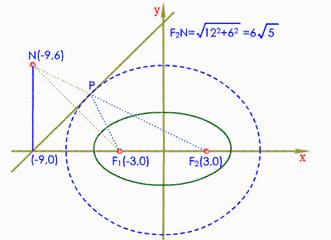
在這值得一提的就是一些推論我們一定要花個心眼去記,比如PF1F2構成的三角形的面積等於tan∠/2(b²),等,這些推論你不弄個十幾分鍾是推不出來的,如果 把他們 牢牢記下,解題會得心應手。
最後 一些考試的小便條;在做橢圓的時候,記住要把你的關鍵式子擺上去,即使運算很難,就那式子是 值得幾分的,有時候你把它的關鍵解決差不多,答案沒算好,沒關係,最多隻是摳你的答案的一倆分,所以步驟寫清楚,思路清晰很重要。
注意事項
做事情時候要有一個良好的心態
要有一個清晰的思路。