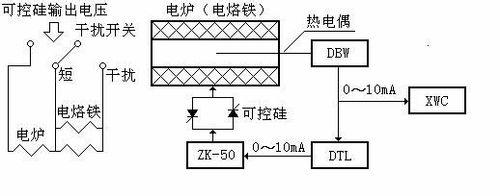
溫度控制系統的組成:
電動溫度控制系統是過程控制系統中常見的一種,其作用是通過一套自動控制裝置,見圖4-1,使爐溫自動維持在給定值。
圖4-1溫度控制系統
爐溫的變化由熱電偶測量,並通過電動溫度變送器轉化為DDZ-Ⅱ型表的標準信號0~10mA直流電流信號,傳送到電子電位差計XWC進行記錄,同時傳送給電動控制器DTL,控制器按偏差的大小、方向,通過預定控制規律的運算後,輸出0~10mA直流電流信號給可控硅電壓調整器ZK-50,通過控制可控硅的導通角,以調節加到電爐(電烙鐵)電熱元件上的交流電壓,消除由於干擾產生的爐溫變化,穩定爐溫,實現自動控制。
工具/原料
比例、比例積分、比例積分微分控制規律的作用,比較餘差及穩定性
A.考察純比例作用(δ=50%,TI=max,TD=0),達到穩定的時間是2’46’’,餘差大小是12mm
B.考察積分作用(δ=50%,TI 1=50s,TD=0),比較積分與比例作用的曲線發現是相互對稱的,餘差的消除時間與比例積分過渡時間基本一致。
C.在PI作用下,系統加入干擾後能消除餘差,然而振盪變劇烈,降低了系統的穩定性。
D.對於擾動作用,考察δ對餘差的影響,由圖比較在(δ=80%,TI=max,TD=0)和在(δ=50%,TI=max,TD=0)控制作用下的兩條曲線可知,δ=80%對應的餘差為33mm>12mm,說明δ越大,餘差越大
E.TI對過渡過程的影響通過比較(δ=50%,TI 1=50s,TD=0)和(δ=50%,TI2=40s,TD=0),發現積分時間越小,積分作用越強,消除餘差越快,振盪加劇,穩定性降低。
F.PID作用下(δ=50%,TI 2=40s,TD=30s),與PI下(δ=50%,TI=40s,TD=0)的控制過程比較,PID作用下的曲線較平穩,穩定性較高,回覆時間短,能較好地實現快速調節過程。
這說明在負荷變化劇烈、擾動幅度大的系統中,適當引入微分作用,可在一定程度上提高系統的控制質量。這是因為當控制器在感受到偏差後再進行控制,過程已經受到較大幅度擾動的影響,而引入微分作用後,當被控變量一有變化時,根據變化趨勢適當加大控制器的輸出信號,將有利於克服擾動對被控變量的影響,抑制偏差的增長,從而提高系統的穩定性。
δ對於過渡過程的影響,綜上分析可知它的值越小,比例控制作用越強,餘差小,當δ減小到1%,實現純比例控制時,將出現發散振盪的情況,這是因為其小於其臨界比例度
步驟/方法
觀察系統各環節的結構、型號、電路的連接,熟悉可控硅電壓調整器和電動控制器上各開關、旋鈕的作用。
控制系統閉環特性的測定:
在以下實驗中使用以下具體數值:δ1(50%),δ2(80%),TI1(50s),TI2(40s),TD1(30s)來觀察比例與積分控制規律的作用
考察比例作用
將δ置於某值50%,記住δ旋鈕在δ1的位置,積分時間置最大(TI=max),微分開關切向0,將干擾開關從“短”切向“干擾”,產生一個階躍干擾(此時為反向干擾),同時在記錄儀的記錄線上作一記號,以記錄階躍干擾加入的時刻,觀察並記錄在純比例作用下達到穩定的時間及餘差大小。
考察積分作用
保持δ=δ1不變,置TI=TI1,同時在記錄儀的記錄線上作一記號,以記錄積分作用加入的時刻,注意觀察積分作用如何消除餘差,直到過程基本穩定。
觀測PI控制作用下的過渡過程
保持δ1,TI1不變,將干擾開關從“干擾”切向“短”,產生一個正向階躍干擾,觀察過渡過程到基本穩定。
考察δ對餘差的影響
置δ=δ2,TI =max,將干擾開關從“短”切向“干擾”,產生一個反向階躍干擾,同時在記錄儀的記錄線上作一記號,以記錄階躍干擾加入的時刻,觀察並記錄在純比例作用下達到穩定的時間及餘差大小。並與1(1)中δ=δ1時的餘差相比較。
再加入積分作用TI=TI 1以消除餘差直到過程基本穩定。
考察TI對過渡過程的影響
置δ=δ1,TI=TI2,將干擾開關從“干擾”切向“短”,產生一個正向階躍干擾,同時在記錄儀的記錄線上作一記號,以記錄階躍干擾加入的時刻,觀察過渡過程到基本穩定,並與2中的實驗結果進行比較,以瞭解TI對過渡過程的影響。
注意:要在同樣條件下才能進行比較,即δ旋鈕的位置要與2中的位置完全一致,才能保證此時的δ1與2中的δ1是相等的
觀測PID控制作用下的過渡過程
保持δ=δ1,TI=TI2不變,置TD=TD1,微分開關切向D,將干擾開關從“短”切向“干擾”,等待過程穩定後,同時在記錄儀的記錄線上作一記號,以記錄階躍干擾加入的時刻,觀察過渡過程,並與PI控制作用下的過渡過程進行比較。
考察δ對穩定性的影響
將δ減小到1%,TI=max,微分開關切向0,觀察過渡過程波動曲線。
7.簡單控制系統的參數整定
採用衰減曲線法(4﹕1)進行參數整定,在純比例(TI=max,微分開關切向0)作用下,δ置於一個較大的數值(30~60%),用改變給定值(一般為5個小格左右)額定值的5%左右,本實驗可改變給定值刻度盤上的五個小格的方法加入階躍輸入,觀察記錄曲線(過渡過程),並計算衰減比,此時衰減比若大於4﹕1,應減小δ值,再用改變給定值的方法加入階躍輸入,觀察記錄曲線,並計算衰減比,直到得到衰減比為4﹕1的過渡過程,記下此時的比例度δS,並通過尺子量出衰減振盪曲線中一個週期的長度,根據記錄儀的走紙速度計算出振盪週期TS,然後根據經驗公式:
δ=1.6δS,
TI=0.4TS
TD=0.2TS
求出相應的δ、TI、TD值,把它們加到控制器中,此時給定值不要變,將干擾開關從“短”切向“干擾”,觀察記錄的(反向階躍)過渡過程曲線,再將干擾開關從“干擾”切向“短”,觀察記錄的(正向階躍)過渡過程曲線,跟各組提供的標準過渡過程曲線(歷屆同學做得最好的過渡過程曲線)相比較,注意正向的與正向的比較,反向的與反向的比較,若有差距,可以適當改變δ、TI、TD值(每次改變δ、TI、TD值,均要記錄),重複以上過程,直到控制系統的控制質量接近或超過標準。
注意事項
在擾動存在時,最後的被控變量與設定值總會存在一定的偏差。
這是因為一旦系統的平衡關係遭到破壞時,控制器必須有一個輸出量才能建立新的平衡關係,而比例控制器的輸出又是正比於輸入e的,因而這時控制器的輸入必然不會為0
b.δ越小,衰減比越小,比例控制作用增強,餘差減小,回覆時間縮短,能較快地將被控變量拉到設定值,但是另一方面,值越小,穩定性會越低,特別是當δ減小到小於其臨界比例度δk時,系統發散振盪,可能會造成事故。
TD越大,微分作用越強,過大則可能會造成系統產生劇烈振盪。
3.繪製一組你在改進控制系統的控制質量的過程中所得到的過渡過程曲線,並註明各參數值。
衰減比4:1下得到的δs=10%,通過尺子量出衰減振盪曲線中一個週期的長度為5.5mm,而走紙速度為300mm/h,故Ts=5.5/300*3600=66s;根據經驗公式
δ=1.6δS=0.16
TI=0.4TS=26.4s
TD=0.2TS=13.2s
把它們加入到控制器中,曲線呈發散,使曲線發散的因素包括δ、TI、TD,根據理論可知在TI越小,TD和δ保持不變的情況下,曲線越容易發散(故後續的值均應往大調)
經過幾組的參數調節,進行質量的控制,涉及的參數如下表所示
序號12345678910δ/%16161313181818161513TI/s26.4303020303028303030TD/s13.213.213.213.213.21515151515