動態規劃將原來具有指數級複雜度的搜尋演算法改進成了具有多項式時間的演算法。其中的關鍵在於解決冗餘,這是動態規劃演算法的根本目的。動態規劃實質上是一種以空間換時間的技術,它在實現的過程中,不得不儲存產生過程中的各種狀態,所以它的空間複雜度要大於其它的演算法。
工具/原料
eclipse-luna
win732bit and jdk1.7
方法/步驟
說明:
在動態規劃中,子問題解決方案被儲存在一個表中,以便這些不必重新計算。 因此,如果這個問題是沒有共同的(重疊)子問題, 動態規劃是沒有用的。例如,二分查詢不具有共同的子問題。
記憶表法:自上而下
打表法:自下而上
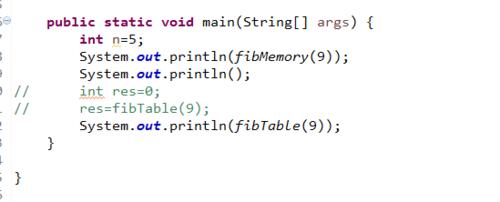
測試main:
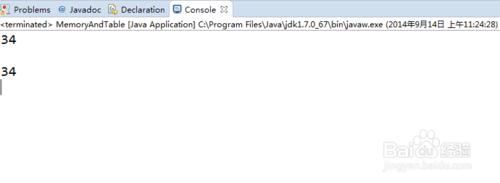
執行結果比較:
完整可執行程式:
/*
* 這一部分程式主要是用來測試記憶化儲存和*/
////記憶表從上而下
public class MemoryAndTable {
static int MAX=20;
static int[] lookUp=new int[MAX];
// public void initMemory(){
// int i;
// lookUp[MAX]=(Integer) null;
// }
public static int fibMemory(int n){
if(lookUp[n]==0){
if(n<=1){
lookUp[n]=n;
}
else{
lookUp[n]=fibMemory(n-1)+fibMemory(n-2);
}
}
return lookUp[n];
}
////打表(自下而上)
public static int fibTable(int n){
int[] f = new int[n+1];
int i;
f[0] = 0;
f[1] = 1;
for(i=2;i<=n;i++){
f[i]=f[i-1]+f[i-2];
}
return f[n];
}
public static void main(String[] args) {
int n=5;
System.out.println(fibMemory(9));
System.out.println();
// int res=0;
// res=fibTable(9);
System.out.println(fibTable(9));
}
}