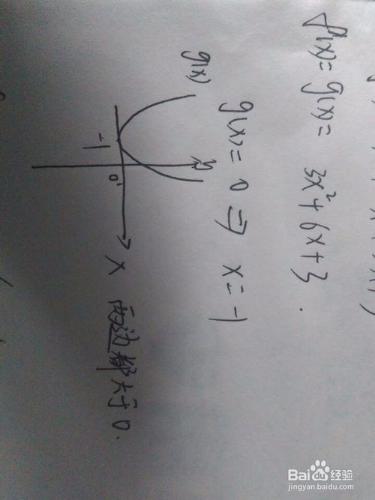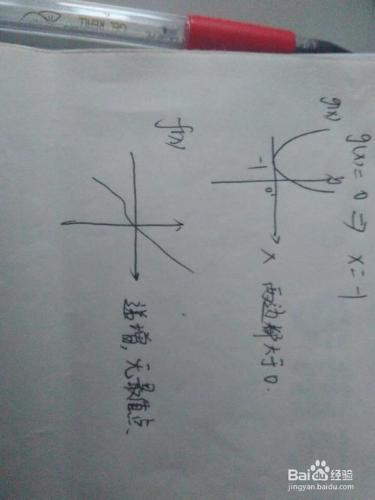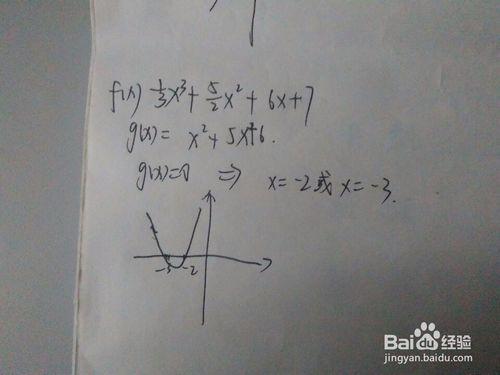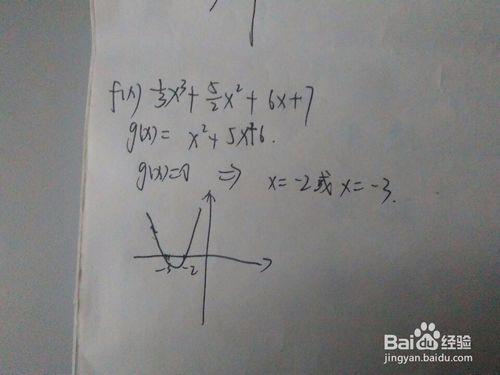求函數f(x)的最值其實很簡單,也有很多方法,比如,如果函數是一元二次函數的話,可以求其對稱軸,對稱軸與函數的交點即為函數的極值點,還比如一次性函數,只要定義域是閉區間或者是半閉區間,那麼最值就是區間的閉端處取;如果函數是一元三次函數或者更復雜的函數,用普通的方法就很難求出結果了。那麼怎麼求複雜函數的最值呢,下面我就給大家介紹一下求這類問題的方法。
工具/原料
紙
筆
方法/步驟
先求其導函數。比如,f(x)=x^3+3x^2+3x+3,用導函數的方法求就是:(設g(x)是fx的導函數,gx=3x^2+6x+3;
令導函數等於0,求解對應的方程。令gx=0,可得x=-1;
根據導函數的函數圖像特徵來判斷該點是極大值點還是極小值點,或者是既不是極大值點也不是極小值點。根據gx的圖像特徵可知,在x=1這一點的左邊gx是大於0的,右邊gx也是大於0的,根據“導函數大於0,函數是遞增的”這一性質,可知fx在定義域內遞增,因此fx沒有極值點,於是更沒有最值點。
再舉一個例子。寫到這個步驟時,突然發現這個函數缺少一般性,不能向讀者展示求複雜函數的一般方法。再舉一個函數吧,fx=(1/3)*(x^3)+(5/2)*(x^2)+6x+7,(定義域是【-7,-1】)這個函數,其導數是x^2+5x+6,令該導數等於0,即求x^2+5x+6=0這個方程,解得x=-2或x=-3;
然後畫出x^2+5x+6這個函數的圖像。可以發現,在x=-2的右側,還有x=-3的左側,導函數都是大於0的,而在-2和-3之間,導函數是小於0的。根據性質有,fx在x<-3或x>-2時是遞增的,而在-3和-2之間是遞減的。
根據函數圖像可知-3是極大值點,-2是極小值點。
再來看看定義域,是【-7,-1】,兩邊都是閉的,於是將兩端的值和極大極小值進行比較,即分別求得f(-7),f(-1),f(-3),f(-2)的值,進行比較,最小的那一個即為最小值,最大的那一個就是最大值。
注意事項
求複雜函數的最值,關鍵就是求其導函數。因此要熟練的掌握導函數的求法。
圖像一點要畫好,否則會導致誤判。