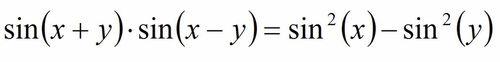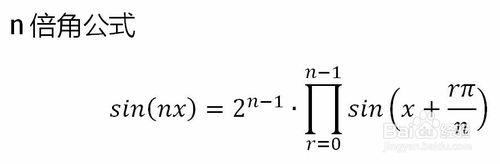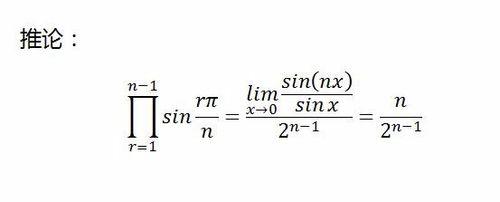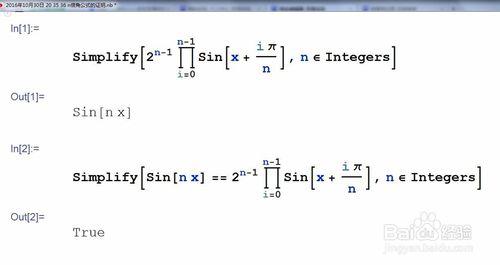n倍角公式是從三角函式的2倍角公式、3倍角公式演化而來的。它在很多數學問題上,都有重要的應用。
工具/原料
演算用的紙、筆
Mathematica(8.0以上版本)
方法/步驟
先來考慮一個函式方程:
設g(x)在複數範圍內處處可導,且對任意複數x,y,恆有:g(x+y)g(x-y)=g^2 (x)-g^2 (y)。求g(x)的解析式!
解答過程如圖,採取的對策是,通過微積分的方法來快捷地處理。
根據上面的結論,可以得到一個簡潔有用的推論。這是正弦函式的內蘊性質:
n倍角公式的定義如下圖。
這個公式的證明過程,採取的對策是用n元一次方程的韋達定理來處理。步驟經過凝縮,如果讀不懂,可以去參考韋達定理、棣莫弗定理。
兩邊同除以sinx,顯然,當x=0時,這是不允許的。但可以用求極限的方法,來處理這個問題。畢竟,極限理論可以處理0/0之流的不定式。
所以有以下推論:
用Mathematica來檢驗n倍角公式的正確性。
程式碼如下:
應用:
用n倍角公式證明二次互反律。這個證明方法,應該是由著名數學家Dirchlet發現的。
應用:
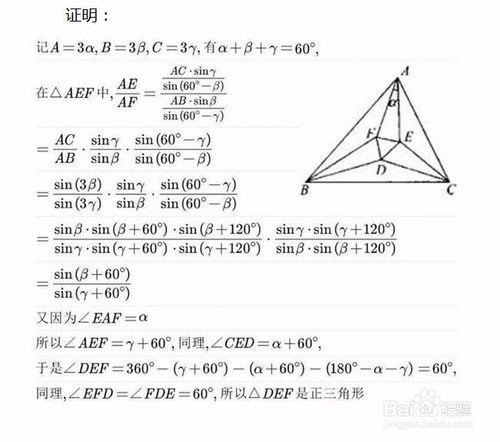
用3倍角公式來證明Morley定理。
如圖:△ABC的三個內角的三等分線交於D、E、F。
求證:△DEF是正三角形。
注意事項
n倍角公式還可以用複變函式的方法來證明。讀者如果有興趣,可以試一下。
Mathematica可以處理很多數學問題,尤其是它的符號計算功能,類似於機器證明。
n倍角公式及其推論,用處還有很多,讀者可自己發掘。