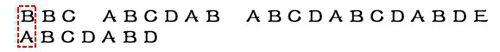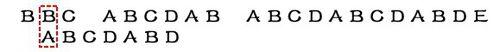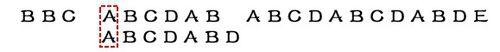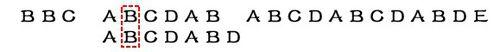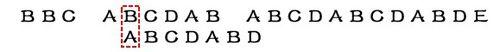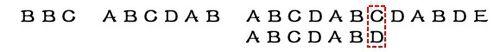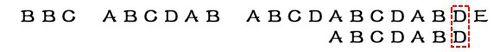KMP算法是一種改進的字符串匹配算法,由D.E.Knuth與V.R.Pratt和J.H.Morris同時發現,因此人們稱它為克努特——莫里斯——普拉特操作(簡稱KMP算法)。KMP算法的關鍵是利用匹配失敗後的信息,儘量減少模式串與主串的匹配次數以達到快速匹配的目的。具體實現就是實現一個next()函數,函數本身包含了模式串的局部匹配信息。
方法/步驟
首先,字符串"BBC ABCDAB ABCDABCDABDE"的第一個字符與搜索詞"ABCDABD"的第一個字符,進行比較。因為B與A不匹配,所以搜索詞後移一位。
因為B與A不匹配,搜索詞再往後移。
就這樣,直到字符串有一個字符,與搜索詞的第一個字符相同為止。
接著比較字符串和搜索詞的下一個字符,還是相同。
直到字符串有一個字符,與搜索詞對應的字符不相同為止。
這時,最自然的反應是,將搜索詞整個後移一位,再從頭逐個比較。這樣做雖然可行,但是效率很差,因為你要把"搜索位置"移到已經比較過的位置,重比一遍。
一個基本事實是,當空格與D不匹配時,你其實知道前面六個字符是"ABCDAB"。KMP算法的想法是,設法利用這個已知信息,不要把"搜索位置"移回已經比較過的位置,繼續把它向後移,這樣就提高了效率。
怎麼做到這一點呢?可以針對搜索詞,算出一張《部分匹配表》(Partial Match Table)。這張表是如何產生的,後面再介紹,這裡只要會用就可以了。
已知空格與D不匹配時,前面六個字符"ABCDAB"是匹配的。查表可知,最後一個匹配字符B對應的"部分匹配值"為2,因此按照下面的公式算出向後移動的位數:
移動位數 = 已匹配的字符數 - 對應的部分匹配值
因為 6 - 2 等於4,所以將搜索詞向後移動4位。
因為空格與C不匹配,搜索詞還要繼續往後移。這時,已匹配的字符數為2("AB"),對應的"部分匹配值"為0。所以,移動位數 = 2 - 0,結果為 2,於是將搜索詞向後移2位。
因為空格與C不匹配,搜索詞還要繼續往後移。這時,已匹配的字符數為2("AB"),對應的"部分匹配值"為0。所以,移動位數 = 2 - 0,結果為 2,於是將搜索詞向後移2位。
逐位比較,直到發現C與D不匹配。於是,移動位數 = 6 - 2,繼續將搜索詞向後移動4位。
逐位比較,直到搜索詞的最後一位,發現完全匹配,於是搜索完成。如果還要繼續搜索(即找出全部匹配),移動位數= 7 - 0,再將搜索詞向後移動7位,這裡就不再重複了。