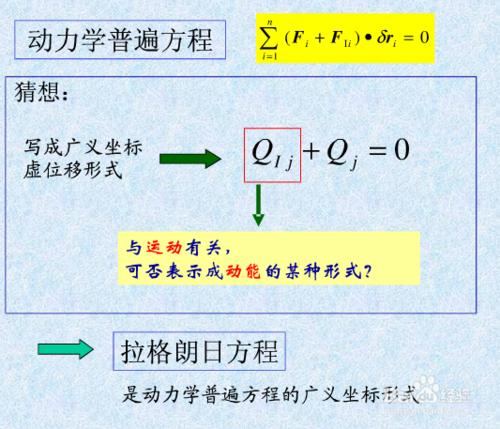
對於建立多自由度振動系統的運動偏微分方程,你是否依然使用經典的牛頓第二定理來推導系統振動方程呢?如果是這樣的話,你就太out,經典牛頓法固然概念明確、方法簡單、物理意義明確,但是它對於複雜的多自由度振動系統進行推導運動方程是不方便的,甚至是十分繁瑣的。但是利用拉格朗日方程法來建立較為複雜的多自由度振動系統的運動偏微分方程是十分簡潔、方便的。下面我們來學習如何用拉格朗日方程法建立振動系統運動方程。
工具/原料
鉛筆、草稿紙
方法/步驟
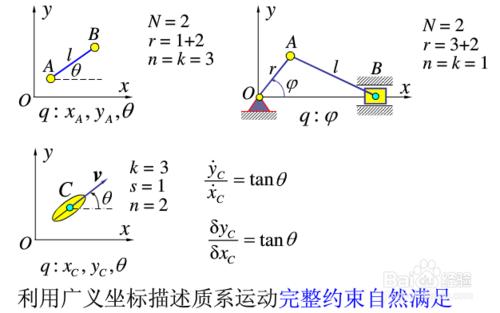
一、廣義座標
物體的機械運動規律可用不同的座標系統表示,我們把秒速系統位形所需要的獨立引數或獨立座標稱為廣義座標,通常用q1,q2,q3,......qn表示,其中n為獨立座標個數。廣義座標具有以下幾種性質:
1. 完備性:廣義座標可以確定系統任意時刻的位形和形狀;
2. 獨立性:同一組廣義座標之間相互獨立、是線性無關的,之間互無函式關係;
3. 不唯一性:一個系統的廣義座標是不唯一的,但個數都等於系統自由度數,且都能用來描述系統的振動規律。
二、廣義力
與廣義座標對應的是廣義力,廣義力是廣義上的力,它的量綱有它與廣義座標虛位移的乘積為功的物理量綱決定的,即:若廣義座標為線位移,則廣義力就是通常意義上的作用力;若廣義座標為角位移,則廣義力就是力矩。
三、拉格朗日方程
根據拉格朗日理論可知,振動系統的運動方程可以用動能 T 、勢能 V 和耗散能 D 表達成下圖所示的表示式:
四、拉格朗日方程法的步驟
利用拉格朗日方程建立系統運動偏微分方程,可以避免未知約束反力的出現,簡化推導過程,其解題步驟可歸納為:
(1) 首先判斷系統的自由度數,並選取適當的廣義座標系;
(2) 以廣義座標和廣義速度建立系統的動能T表示式;
(3) 當主動力是保守力,建立用廣義座標表示的只能U的表示式;
(4) 對於有阻尼情況,應該單獨考慮阻尼,計算相應廣義速度對應的耗散能函式D;
(5) 當有非保守力時,計算廣義座標qi對應的廣義力Qi
(6) 將T、V、D和Qi ,代入拉格朗日方程進行運算,即可得到振動系統的運動偏微分方程。
五、算例分析
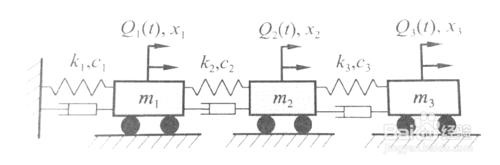
建立如下圖1所示的三自由度質量-阻尼-彈簧振動系統的振動方程。
解:如圖所示,建立座標系,眼水平振動方向選擇廣義座標系(x1,x2,x3),則按上節所述步驟,依次求解。求解過程如下圖2所示。
注意事項
注意系統是否有非保守力對應的廣義力
系統是否存在能力耗散